CF377C Captains Mode

洛谷传送门 CF传送门

Solution

很显然的，两个队列肯定选择最强的，即使 (m) 个操作均为‘b’操作，这些操作也只和最强的 (m) 个英雄有关。

发现题目中 (mleq min(n,20)) ，所以可以考虑状压DP。

在DP之前，还有一点问题——跳过‘p’和'b'怎么办？

对于跳过‘p’，因为两边都是最优策略，所以自己选择一定比随机优；对于跳过‘b’，就相当于禁了最弱的那个，没有影响。

那么现在操作只有‘p’和'b'，设 (dp_{st,pos}) 表示当前状态是 (st) ，现在是第 (pos) 个操作，（一队减二队）最大的得分。对于操作 (i) ，如果 (i) 和 (i-1) 是一个队的操作，最优一定是相加；如果不是，最优一定是做差。

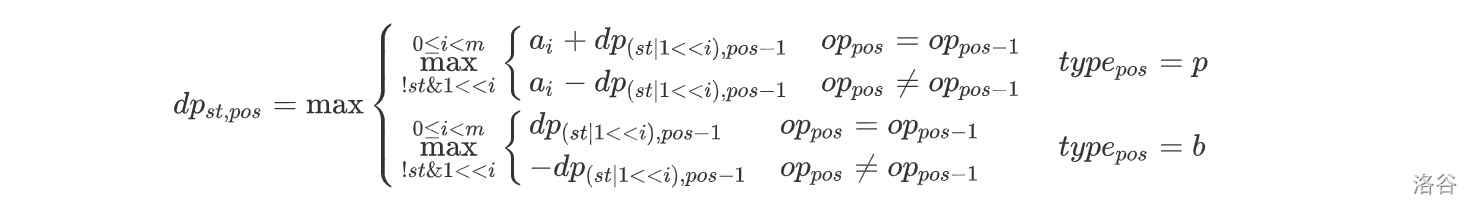
(关于我的博客 (LaTeX) 又锅了这件事)

其中 (op_{pos}) 表示是哪个队操作的， (type_{pos}) 表示是哪种操作。

肉眼可见，这个转移方程分类讨论了许多，所以选择拿记忆化搜索来转移。(￣▽￣)"

注意：因为刚开始的 (dp_{0,m-1}) 我们是默认 (op_{m-1}=1) 来做的，所以如果 (op_{m-1}=2) ，在求完 (dp_{0,m-1}) 后要取反。

Code

#include<bits/stdc++.h>

using namespace std;
const int N=1<<20,INF=0x3f3f3f3f;
int dp[N][20],n,m,a[110],type[50],op[50];
bool vis[N][20];
char s[5];

int  dfs(int st,int pos){
    if(vis[st][pos]) return dp[st][pos];
    vis[st][pos]=true;
    int & ans=dp[st][pos];
    ans=-INF;
    if(type[pos]){
        for(int i=0;i<m;i++){
            if((1<<i)&st) continue;
            if(pos==0) ans=max(ans,a[i]);
            else if(op[pos]==op[pos-1])
                      ans=max(ans,a[i]+dfs(st|(1<<i),pos-1));
                 else ans=max(ans,a[i]-dfs(st|(1<<i),pos-1));
        }
    }
    else{
        for(int i=0;i<m;i++){
            if((1<<i)&st) continue; 
            if(pos==0) ans=max(ans,0);
            else if(op[pos]==op[pos-1])
                      ans=max(ans,dfs(st|(1<<i),pos-1));
                 else ans=max(ans,-dfs(st|(1<<i),pos-1));
        }
    }
    return ans;
}

int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    scanf("%d",&m);
    for(int i=m-1;i>=0;i--){
        scanf("%s%d",s,&op[i]);
        type[i]=(s[0]=='p');
    }
    sort(a,a+n);
    for(int i=0;i<m;i++)
        swap(a[i],a[n-i-1]);
    int ans=dfs(0,m-1);
    if(op[m-1]==2) ans=-ans;//取反
    printf("%d
",ans);
    return 0;
}