Hausdorff distance between mesh and its symmertic one.

When talking about distances, we usually mean the shortest :   for instance, if a point X is said to be at distance D of a polygon P, we generally assume that D is the distance from X to the nearest point of P. The same logic applies for polygons :  if two polygons A and B are at some distance from each other, we commonly understand that distance as the shortest one between any point of A and any point of B.  Formally, this is called a minimin function, because the distance D between A and B is given by :

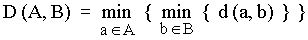(eq. 1)

This equation reads like a computer program : « for every point a of A, find its smallest distance to any point b of B ;  finally, keep the smallest distance found among all points a ».

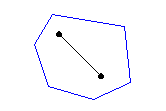
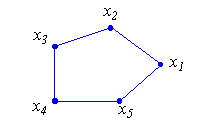
That definition of distance between polygons can become quite unsatisfactory for some applications ;  let's see for example fig. 1.  We could say the triangles are close to each other considering their shortest distance, shown by their red vertices. However, we would naturally expect that a small distance between these polygons means that no point of one polygon is far from the other polygon.   In this sense, the two polygons shown in fig. 1 are not so close, as their furthest points, shown in blue, could actually be very far away from the other polygon. Clearly, the shortest distance is totally independent of each polygonal shape.

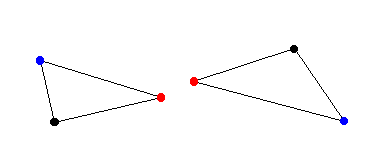
Figure 1 :

The shortest distance doesn't consider the whole shape.

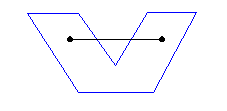
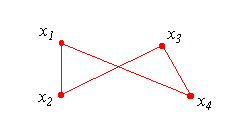
Another example is given by fig. 2, where we have the same two triangles at the same shortest distance than in fig. 1, but in different position.  It's quite obvious that the shortest distance concept carries very low informative content, as the distance value did not change from the previous case, while something did change with the objects.

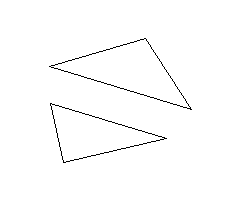
Figure 2 :

The shortest distance doesn't account for the position of the objects.

As we'll see in the next section, in spite of its apparent complexity, the Hausdorff distance does capture these subtleties, ignored by the shortest distance.

2.  What is Hausdorff distance ? 

Named after Felix Hausdorff (1868-1942), Hausdorff distance is the «  maximum distance of a set to the nearest point in the other set » [Rote91]. More formally, Hausdorff distance from set A to set B is a maximin function, defined as

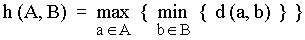(eq. 2)

where a and b are points of sets A and B respectively, and d(a, b) is any metric between these points ; for simplicity, we'll take d(a, b) as the Euclidian distance between a and b. If for instance A and B are two sets of points, a brute force algorithm would be :

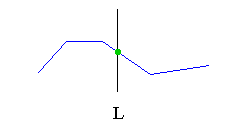
Brute force algorithm : 1.  h = 0  2.  for every point ai of A,       2.1  shortest = Inf ;       2.2  for every point bj of B                     dij = d (ai , bj )                     if dij < shortest then                               shortest = dij       2.3  if shortest > h then                      h = shortest

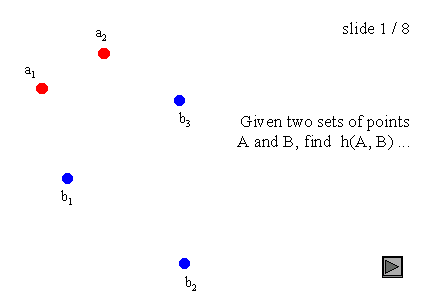
Figure 3 :   Hausdorff distance on point sets.

This is illustrated in fig. 3 : just click on the arrow to see the basic steps of this computation. This algorithm obviously runs in O(n m) time, with n and m the number of points in each set. 

It should be noted that Hausdorff distance is oriented (we could say asymmetric as well), which means that most of times h(A, B) is not equal to h(B, A). This general condition also holds for the example of fig. 3, as h(A, B) = d(a1, b1), while h(B, A) = d(b2, a1). This asymmetry is a property of maximin functions, while minimin functions are symmetric.

A more general definition of Hausdorff distance would be :

H (A, B) = max { h (A, B), h (B, A) }

(eq. 3)

which defines the Hausdorff distance between A and B, while eq. 2 applied to Hausdorff distance from A to B (also called directed Hausdorff distance). The two distances h(A, B) and h(B, A) are sometimes termed as forward and backward Hausdorff distances of A to B. Although the terminology is not stable yet among authors, eq. 3 is usually meant when talking about Hausdorff distance. Unless otherwise mentionned, from now on we will also refer to eq. 3 when saying "Hausdorff distance".

If sets A and B are made of lines or polygons instead of single points, then H(A, B) applies to all defining points of these lines or polygons, and not only to their vertices. The brute force algorithm could no longer be used for computing Hausdorff distance between such sets, as they involve an infinite number of points.

So, what about the polygons of fig. 1 ? Remember, some of their points were close, but not all of them. Hausdorff distance gives an interesting measure of their mutual proximity, by indicating the maximal distance between any point of one polygon to the other polygon. Better than the shortest distance, which applied only to one point of each polygon, irrespective of all other points of the polygons.

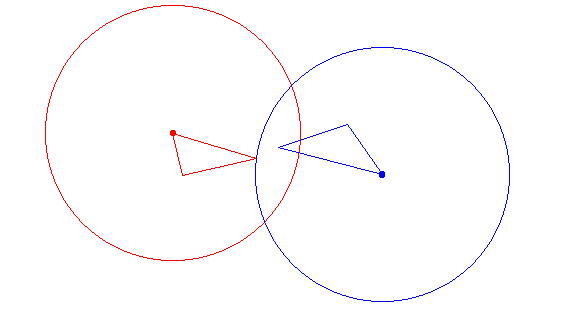
Figure 4 :

Hausdorff distance shown around extremum of each triangles of fig. 1. Each circle has a radius of H( P1 , P2).

The other concern was the insensitivity of the shortest distance to the position of the polygons. We saw that this distance doesn't consider at all the disposition of the polygons.  Here again, Hausdorff distance has the advantage of being sensitive to position, as shown in fig.5. 

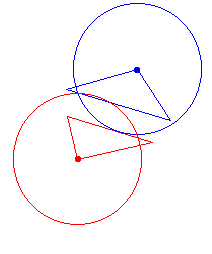
Figure 5 :

Hausdorff distance for the triangles of fig. 4 at the same shortest distance, but in different position.

3.  Computing Hausdorff distance between convex polygons

3.1  Assumptions

Throughout the rest of our discussion, we assume the following facts about polygons A and B :

• Polygons A and B are simple convex polygons ;
  
  
• Polygons A and B are disjoint from each other, that is :
  
    - they don't intersect together ; 
    - no polygon contains the other.
  
  

3.2  Lemmas

The algorithm explained in the next section is based on three geometric observations, presented here. In order to simplify the text, we assume two points a and b that belong respectively to polygons A and B, such that :

d (a, b) = h (A, B)

In simple words, a is the furthest point of polygon A relative to polygon B, while b is the closest point of polygon B relative to polygon A.

Lemma 1a :

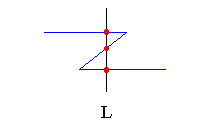
The perpendicular to ab at a is a supporting line of A, and A is on the same side as B relative to that line. Proof of lemma 1a

Lemma 1b :

The perpendicular to ab at b is a supporting line of B, and a and B are on different sides relative to that line. Proof of lemma 1b

Lemma 2 :

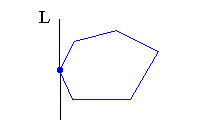
There is a vertex x of A such that the distance from x to B is equal to h (A, B). Proof of lemma 2

Lemma 3 :

Let bi be the closest point of B from a vertex a i  of A.  If µ is the moving direction (clockwise or counterclockwise) from bi to bi+1 then, for a complete cycle through all vertices of A, µ changes no more than twice. Proof of lemma 3

3.3  Algorithm

The algorithm presented here was proposed by [Atallah83].  Its basic strategy is to compute successively h(A,B) and h(B, A) ;  because of lemma 2, there is no need to query every point of the starting polygon, but only its vertices. 

An important fact used by this algorithm is that a closest point can only be a vertex of the target polygon, or the foot z of a line perpendicular to one of its edges.  This fact suggests a function to check for the existence of a possible closest point. Given a source point a and a target edge defined by a point b1 and a vertex b2 :

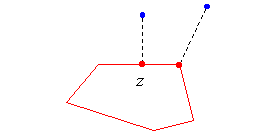Function z = CheckForClosePoint (a, b1 , b2 ) :

Compute the position z where the line that passes through b1 and b2 crosses its perpendicular through a  ;
if z is between b1 b2 then return z ;
else compute at b2 a line P perpendicular to the line ab2 ;
        if P is a supporting line of B then return b2 ;
        else return NULL. 

That function obviously uses lemma 1b to decide whether or not the closest point of B might be located on the target edge, that should be close to a.  It also supposes that the source point a and b2 are not located on different sides of the perpendicular to [b1b2 ] at b1, accordingly to lemma 3. 

Now we are ready for the main algorithm ; the vertices of both polygons are presumed to be enumerated counterclockwise :

Algorithm for computing h(A, B) :

1.  From a1, find the closest point b1 and compute d1 = d ( a1, b1 )
2.  h(A, B) = d1
3.  for each vertex ai of A,
      3.1  if ai+1 is to the left of aibi
                     find bi+1 , scanning B counterclockwise with CheckForClosePoint from bi
              if ai+1 is to the right of aibi
                     find bi+1 , scanning B clockwise with CheckForClosePoint from bi
              if ai+1 is anywhere on aibi
                      bi+1 = bi
      3.2  Compute di+1 = d (ai+1 , bi+1 )
      3.3  h (A, B) = max { h (A, B), di+1 }

3.4  Complexity

If polygons A and B respectively have n and m vertices, then :

• Step 1 can clearly be done in O(m) time ;
• Step 2 takes constant time O(1) ;
• Step 3 will be executed (n-1) times, that is O(n) ;
• Step 3.1 will not be executed in total more than O(2m). This is a consequence of lemma 3, which guarantees that polygon B can not be scanned more than twice ;
• Steps 3.2 and 3.3 are done in constant time O(1) ;

So the algorithm for computing h(A, B) takes :

O(m) + O(n) + O(2m) = O(n+m)

To find H(A, B), the algorithm needs to executed twice ;  the total complexity for computing Hausdorff distance then stays linear to O(n+m).

3.5  Interactive applet

This applet illustrates the algorithm for computing h(A,B). You only need to draw two polygons, and then press the "step" or "run" button. Left click to define a new vertex, and close the polygon by clicking near the first vertex. Polygon A is the first one you draw, in green, while polygon B appears next, in red. 

The algorithm was slightly modified to make it more appealing visually. Even if this algorithm is intended for two polygons totally separated from each other, it also works when B is inside A. However, it won't work if A is inside of B, or when A and B are partially intersecting. You're allowed anyway to try these cases to see what happens ! 

When defining your polygons, you will see a yellow area that indicates where you can add the next vertex, so the polygon keeps convex. The applet won't let you define a non-convex polygon. 

Please notice that the first time you draw the second half of a polygon, you will have to wait a few seconds until the Jama package loads. 

Java Applet

Source code

Documentation of the classes

4.  Application examples

One of the main application of the Hausdorff distance is image matching, used for instance in image analysis, visual navigation of robots, computer-assisted surgery, etc. Basically, the Hausdorff metric will serve to check if a template image is present in a test image ;  the lower the distance value, the best the match. That method gives interesting results, even in presence of noise or occlusion (when the target is partially hidden). 

Say the small image below is our template, and the large one is the test image : 

We want to find if the small image is present, and where, in the large image. The first step is to extract the edges of both images, so to work with binary sets of points, lines or polygons : 

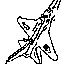Edge extraction is usually done with one of the many edge detectors known in image processing, such as Canny edge detector, Laplacian, Sobel, etc. After applying Rucklidge's algorithm that minimizes Hausdorff distance between two images, the computer found a best match : 

For this example, at least 50 % of the template points had to lie within 1 pixel of a test image point, and vice versa. Some scaling and skew were also allowed, to prevent rejection due to a different viewing angle of the template in the test image (these images and results come from Michael Leventon's pages). Other algorithms might allow more complicated geometric transformations for registering the template on the test image. 

In spite of my interest for the topic, an online demo is definitely beyond the scope of this Web project !  So here are some Web resources about image matching with Hausdorff distance : 

• Hausdorff-based image comparison 
  A vision project that uses the generalized Hausdorff distance
  to locate a template image in an indoor scene.
  
  
• Hausdorff distance for object tracking and classification 
  Hausdorff distance used with a multi-layer perceptron 
  for recognizing and tracking cars in a road scene.
  
  
• Computer-vision-enabled ophthalmic augmented reality environment 
  An interesting application of Hausdorff distance for merging
  partially overlapping images into a single image.
  
  
• Comparing 2D images of the 3D world 
  Conference material by Daniel Huttenlocher on object recognition.
  Briefly introduces some problems of image analysis, and compares
  the generalized Hausdorff distance with more traditional methods.
  
  

---

Glossary

Convex polygon :   

A polygon is said convex if the line that joins any two points of the polygon is entirely inside the polygon.

Convex polygon

Non-convex polygon

Metric :

A function D, usually called distance, that respects the following properties when applied to x, y and z :

1.  D(x, y) >= 0	(positiveness)
2.  D(x, y) = 0 iff x = y	(identity)
3.  D(x, y) = D(y, x)	(symmetry)
4.  D(x, y) + D(y, z) >= D(x, z)	(triangle inequality)

Monotone chain :

A chain C (i.e. a sequence of edges) is said to be monotone in a direction D if any line L orthogonal to D intersects C in exactly one point.

Monotone chain

Non-monotone chain

A polygon P is monotone in some direction if an orthogonal line intersects P in no more than two points ;  a convex polygon is monotone in any direction. 

Simple polygon :

A polygon with no self-intersecting edges. Since a polygon is defined by a sequence of vertices, a priori nothing prevents any self-intersection of its edges. 

Simple polygon

Non-simple polygon

Supporting line :

Straight line L passing through a vertex of a polygon P, such that the interior of P lies entirely on one side of L.  The supporting line is a generalization of the tangent. 

References

No, I didn't use all of these references ! Most of this project was inspired by Atallah. Anyway, here is a listing of everything I found, as of Dec. 98, about algorithms on Hausdorff distance and image matching. Hope you can find some good material for yourself. 

1. H. Alt (1994). Matching shapes with a reference point. Technical report B 94-18, Institut für Informatik, Freie Universität Berlin, DE. 
   
   

2. H. Alt, B. Behrends, J. Blömer (1992). Approximate matching of polygonal shapes. Technical report B 93-10, Institut für Informatik, Freie Universität Berlin, DE. 16 pages. 
   
   

3. M. J. Atallah (1983). A linear time algorithm for the Hausdorff distance between convex polygons. Information Processing Letters, v. 17, pp. 207-209. 
   
   

4. M. Beauchemin, K. P. B. Thomson, G. Edwards (1998). On the Hausdorff distance used for the evaluation of segmentation results. Canadian Journal of Remote Sensing, v. 24(1), pp. 3-8. Also appeared in Proc. Int. Symp. on Geomatics in the Era of Radarsat (GER'97, Ottawa, CA). 
   
   

5. E. Belogay, C. Cabrelli, U. Molter, R. Shonkwiler (1997). Calculating the Hausdorff distance between curves. Information Processing Letters, v. 64, pp. 17-22. 
   
   

6. I. Bloch (1996). Fu geodesic distance in images. In T. Martin and A. Ralescu (ed.), Lecture Notes In Artificial Intelligence v. 1188 : Fu Logic in Artificial Intelligence, towards Intelligent Systems, Springer, pp. 153-166. 
   
   

7. L. P. Chew, K. Kedem (1998). Getting around a lower bound for the minimum Hausdorff distance. Computational Geometry, Theory and Applications, v. 10(3), pp. 197-202. 
   
   

8. L. P. Chew, K. Kedem, S. Schirra (1994). On characteristic points and approximate decision algorithms for the minimum Hausdorff distance. Technical report MPI-I-94-150, Max-Planck-Institut für Informatik, Saarbrücken, DE. 10 pages. 
   
   

9. M. P. Dubuisson, A. K. Jain (1994). Modified Hausdorff distance for object matching. Proc. of IAPR Int. Conf. on Pattern Recognition (ICPR'94, Jerusalem, IS), v. A, pp. 566-568. 
   
   

10. P. W. Goldberg (1993). PAC-learning geometrical figures. Ph.D. thesis, Lab. for foundations of computer science, University of Edinburgh, UK. 
    
    

11. W. E. Grimson, D. P. Huttenlocher (1994). Analyzing the probability of a false alarm for the Hausdorff distance under translation. Proc. of Image Understanding Workshop (ARPA'94, Monterey, CA), v. II, pp. 1257-1262. 
    
    

12. D. P. Huttenlocher, K. Kedem (1990). Computing the minimum Hausdorff distance for point sets under translation. Proc. of 6th Annual ACM Symp. on Comp. Geom. (SCG'90, Berkeley, CA), pp. 340-349. 
    
    

13. D. P. Huttenlocher, K. Kedem, J. M. Kleinberg (1992). On dynamic Voronoi diagrams and the minimum Hausdorff distance for point sets under Euclidian motion in the plane. Proc. of 8th Annual ACM Symp. on Comp. Geom. (SCG'92, Berlin, DE), pp. 110-119. Also known as tech. report TR 92-1271, Dept. of computer science, Cornell University, NY. 
    
    

14. D. P Huttenlocher, G. A. Klanderman, W. J. Rucklidge (1993). Comparing images using the Hausdorff distance. IEEE Trans. on Pattern Analysis and Machine Intelligence, 15(9), pp. 850-863. Also appeared in CVPR'92, pp. 654-656, under Comparing images using the Hausdorff distance under translation. 
    
    

15. D. P. Huttenlocher, R. H. Lilien, C. F. Olson (1996). Approximate Hausdorff matching using Eigenspaces. Proc. of Image Understanding Workshop (ARPA'96, Palm Springs, CA), pp. 1181-1186. Also appeared in Proc. of European Conf. on Computer Vision, pp. 536-545 (1996). 
    
    

16. D. P. Huttenlocher, W. J. Rucklidge (1992). A multi-resolution technique for comparing images using the Hausdorff distance. Tech. report TR 92-1321, Dept. of Computer science, Cornell University, NY. 20 pages. Also appeared in Proc. of CVPR'93. 
    
    

17. K. Kedem, Y. Yarmovski (1996). Curve based stereo matching using the minimum Hausdorff distance. Proc. of 12th Annual ACM Symp. on Comp. Geom. (SCG'96, Philadelphia, PA), pp. 415-418. 
    
    

18. R. Lusinyants, A. Gross, E. Oranskaya (1998). Applications of geometric edge filtering and Hausdorff variations in finding and classifying image structure. Submitted to Workshop on Applied Computer Vision. 
    
    

19. C. F. Olson (1998). Probabilistic formulation for Hausdorff matching. Proc. of IEEE Conf. on Vision and Pattern Recognition (CVPR'98, Santa Barbara, CA), pp. 150-156. 
    
    

20. J. Paumard, E. Aubourg (1997). Adjusting astronomical images using a censored Hausdorff distance. Proc. of 4th IEEE Int. Conf. on Image Processing (ICIP '97, Santa Barbara, CA), v. III, pp. 232-xxx. 
    
    

21. F. P. Preparata, M. I. Shamos (1985). Computational geometry, an introduction. Springer-Verlag, NY. 398 pages. 
    
    

22. G. Rote (1991). Computing the minimum Hausdorff distance between two point sets on a line under translation. Information Processing Letters, v. 38, pp. 123-127. 
    
    

23. W. Rucklidge (1995). Lower bounds for the complexity of Hausdorff distance. Tech. report TR 94-1441, Dept. of computer science, Cornell University, NY. A similar title appeared in Proc. 5th Canad. Conf. on Comp. Geom. (CCCG'93, Waterloo, CA), pp. 145-150. 
    
    

24. W. Rucklidge (1995). Efficient computation of the minimum Hausdorff distance for visual recognition. Ph.D. thesis, Dept. of computer science, Cornell University, NY. 
    
    

25. W. J. Rucklidge (1995). Locating objects using the Hausdorff distance. Proc. of 5th Int. Conf. on Computer Vision (ICCV'95, Cambridge, MA), pp. 457-464. 
    
    

26. W. J. Rucklidge (1996). Efficient visual recognition using the Hausdorff distance. Lecture Notes in Computer Science, no 1173, Springer-Verlag, NY. 
    
    

27. W. J. Rucklidge (1997). Efficiently locating objects using the Hausdorff distance. Int. J. of Computer Vision, 24(3), pp. 251-270. 
    
    

28. R. Shonkwiler (1989). An image algorithm for computing the Hausdorff distance efficiently in linear time. Information Processing Letters, v. 30, pp. 87-89. 
    
    

29. R. Shonkwiler (1991). Computing the Hausdorff set distance in linear time for any Lp point distance. Information Processing Letters, v. 38, pp. 201-207. 
    
    

30. J. H. Yi, B. Bhanu, M. Li (1996). Target indexing in SAR images using scattering centers and the Hausdorff distance. Pattern Recognition Letters, v. 17(11), pp. 1191-1198 
    
    

31. X. Yi, O. C. Camps (1995). Line feature-based recognition using the Hausdorff distance. Proc. of IEEE Symp. on Computer Vision (SCV'95, Miami Beach, FL), pp. 79-84. 
    
    

32. X. Yi, O. C. Camps (1997). Robust occluding contour detection using the Hausdorff distance. Proc. of IEEE Conf. on Vision and Pattern Recognition (CVPR'97, San Juan, PR), pp. 962-967.