两个信号在时域的卷积等于频域的乘积。而二维图像常用的滤波处理,就是二维图像与一个3*3或者5*5的滤波数组(又常称为模板或者卷积核)的卷积,
对应于该二维图像与滤波数组经过变换(最常用的是傅里叶变换)到频域后数据的乘积。正式因为这个数学特征,使得我们在时域看起来很难处理的频率
滤波,在频域非常容易得以实现。
通过下面的3张图,很容易理解图像数据里高频信号和低频信号的概念:
1.原图及傅里叶变换幅度图(左下)与相位图(右下)

2.傅里叶变换幅度图中心圆外面部分(高频部分)全零与反傅里叶变换后的原图

3.傅里叶变换幅度图中心圆里面部分(低频部分)全零与反傅里叶变换后的原图
 、
、
【附录】
图像滤波 ,即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,是图像预处理中不可缺少的操作,其处理效果的好坏将直接响到后续图像处理和分析的有效性和可靠性。滤波就是要去除没用的信息,保留有用的信息,可能是低频,也可能是高频 。滤波的目的有两个:一是抽出对象的特征作为图像识别的特征模式; 另一个是为适应图像处理的要求,消除图像数字化时所混入的噪声。
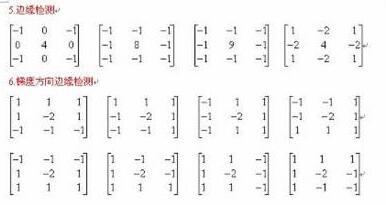
常用的几种滤波数组(如果不想改变图像的亮度,注意数组的系数总和要等于1。例如低通滤波第一组数据要乘以1/9):