堆操作
实验目的
(一)建堆:将数组A[1..n]变成一个最大堆。
(二)堆排序:将一个堆中的元素按递减排序输出。
(三)用插入方法建堆:堆大小从1到n每次插入一个元素到堆中,直到n个元素入堆。
实验原理
(二叉)堆是一个数组,它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外,该树是完全充满的,而且是从左向右填充。表示堆的数组A包括两个属性:A.length(通常)给出数组元素的个数,A.heap-size表示有多少个堆元素存储在该数组中。也就是说,虽然A[1..A.length]可能都存有数据,但是只有A[1..A.heap-size]中存放的是堆的有效元素,这个,0 <=A.heap-size <= A.length 。树的根节点是A[1]。
二叉堆可以分为两种形式:最大堆和最小堆。在这两种堆中,结点的值都要满足堆的性质,但一些细节定义则有所差异。在最大堆中,最大堆性质是指除了根以外的所有结点i都要满足:A[PARENT(i)] >= A[i] ,也就是说,某个结点的值至多与其父结点一样大。因此,堆中的最大元素存放在根结点中;并且,在任一子树中,该子树所包含的所有结点的值都不大于该子树根节点的值。最小堆的组织方式正好相反:最小堆性质是指除了根以外的所有结点i都有A[PARENT(i)] <= A[i] ,最小堆中的最小元素存放在根结点中。
实验过程
(一)维护堆的性质
MAX-HEAPIFY是用于维护最大堆性质的重要过程。它的输入为一个数组A和一个下标i。在调用MAX-HEAPIFY的时候,对于违背了最大堆的性质的A[i]使其在最大堆中“逐级下降”,从而使得以下标i为根结点的子树重新遵循最大堆的性质。
MAX-HEAPIFY(A, i)
1 l = LEFT(i)
2 r = RIGHT(i)
3 if l <= A.heap-size andA[l] > A[i]
4 largest = l
5 else largest = i
6 if r <= A.heap-size andA[r] > A[largest]
7 largest = r
8 if largest != i
9 exchange A[i] with A[largest]
10 MAX-HEAPIFY(A, largest)
(二)建堆
我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n = A.length的数组A[1..n]转换为最大堆。子数组A(|n/2|+1..n)中的元素都是树的叶节点。对每一个叶节点都调用MAX-HEAPIFY进行调整,从而满足最大堆的性质。
BUILD-MAX-HEAP
1 A.heap-size = A.length
2 for i = |A.length/2| downto1
3 MAX-HEAPIFY(A, i)
(三)堆排序
由于数组中的最大元素总是在根结点A[1]中,通过把它与A[n]进行互换,我们可以让该元素放到正确的位置。这个时候,我们从堆中去掉结点n(即通过减少A.heap-size的值来实现),剩余的节点中,原来根的孩子仍然是最大堆,而新的节点可能违背最大堆的性质,为了维护最大堆的性质,调用一次MAX-HEAPIFY(A, 1),从而在A[1..n-1]上构造一个新的最大堆。
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i = A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size = A.heap-size - 1
5 MAX-HEAPIFY(A, 1)

(四)插入方法建堆
MAX-HEAP-INSERT能够实现INSERT操作。它的输入是要被插入到最大堆A中的新元素的关键字。MAX-HEAP-INSERT首先通过增加一个关键字为-∞的叶节点来扩展最大堆,然后调用HEAP-INCREASE-KEY为新节点设置对应的关键字,同时保持最大堆的性质。
MAX-HEAP-INSERT(A, key)
1 A.heap-size = A.heap-size +1
2 A[A.heap-size] = -∞
3 HEAP-INCREASE-KEY(A,A.heap-size, key)
HEAP-INCREASE-KEY(A, i, key)
1 if key < A[i]
2 error“new key is smaller than current key”
3 A[i] = key
4 while i > 1 and A[PARENT(i)]< A[i]
5 exchange A[i] with A[PARENT(i)]
6 i = PARENT(i)
实验总结
(一)将整个实验过程完成后,深入理解了二叉堆的性质。堆的优点:在大多数计算机上,在实现PARENT(i),LEFT(i),RIGHT(i)过程中,可以通过较少的指令(左移,右移)进行计算。
(二)在建堆的过程中,有一个巧妙的地方:就是对于A[|A.length/2|..1]的叶节点进行最大堆的性质维护,而不是遍历整个堆。
(三)堆排序的实际应用场景:基于最大堆实现最大优先队列(记录将要执行的各个作业以及它们之间的相对优先级),从而应用到计算机系统的作业调度中。
附录(代码)
(一)建堆
1 #include <stdio.h> 2 3 #include <stdlib.h> 4 5 6 7 #define a_length 10 8 9 10 11 int a_heap_size; 12 13 14 15 void max_heapify(int a[], int i){ 16 17 intl,r,largest; 18 19 int change; 20 21 l = 2 * i +1; 22 23 r = 2 * i +2; 24 25 if(l <=a_heap_size-1 && a[l] > a[i]) 26 27 largest =l; 28 29 else largest= i; 30 31 if(r <=a_heap_size-1 && a[r] > a[largest]) 32 33 largest =r; 34 35 if(largest !=i){ 36 37 change = a[i]; 38 39 a[i] = a[largest]; 40 41 a[largest]= change; 42 43 max_heapify(a,largest); 44 45 } 46 47 } 48 49 50 51 void build_max_heap(int a[]){ 52 53 int i; 54 55 a_heap_size =a_length; 56 57 for(i =a_length/2 - 1; i >= 0; i--) 58 59 max_heapify(a,i); 60 61 } 62 63 64 65 int main(){ 66 67 inta[a_length] = {4,1,3,2,16,9,10,14,8,7}; 68 69 int i; 70 71 72 73 printf("origin_heapa[]="); 74 75 for(i = 0; i< 10; i++) 76 77 printf("%d ",a[i]); 78 79 printf(" "); 80 81 82 83 build_max_heap(a); 84 85 86 87 printf(" max_heap a[]="); 88 89 for(i = 0; i< 10; i++) 90 91 printf("%d ",a[i]); 92 93 printf(" "); 94 95 }
(二)堆排序
1 #include <stdio.h> 2 3 #include <stdlib.h> 4 5 6 7 #define a_length 10 8 9 10 11 int a_heap_size; 12 13 14 15 void max_heapify(int a[], int i){ 16 17 intl,r,largest; 18 19 int change; 20 21 l = 2 * i +1; 22 23 r = 2 * i +2; 24 25 if(l <=a_heap_size-1 && a[l] > a[i]) 26 27 largest =l; 28 29 else largest= i; 30 31 if(r <=a_heap_size-1 && a[r] > a[largest]) 32 33 largest =r; 34 35 if(largest !=i){ 36 37 change = a[i]; 38 39 a[i] = a[largest]; 40 41 a[largest]= change; 42 43 max_heapify(a,largest); 44 45 } 46 47 } 48 49 50 51 void build_max_heap(int a[]){ 52 53 int i,j; 54 55 a_heap_size =a_length; 56 57 for(i =a_length/2 - 1; i >= 0; i--) 58 59 max_heapify(a,i); 60 61 } 62 63 64 65 void heapsort(int a[]){ 66 67 inti,exchange; 68 69 int j; 70 71 for(i =a_length-1; i >= 1; i--){ 72 73 exchange = a[0]; 74 75 a[0] = a[i]; 76 77 a[i] = exchange; 78 79 a_heap_size= a_heap_size - 1; 80 81 82 83 max_heapify(a,0); 84 85 86 87 printf(" a_heap_size= %d i = %d ",a_heap_size,i); 88 89 for(j = 0;j < 10; j++) 90 91 printf("%d ",a[j]); 92 93 printf(" "); 94 95 96 97 } 98 99 } 100 101 102 103 104 105 int main(){ 106 107 int a[a_length] = {4,1,3,2,16,9,10,14,8,7}; 108 109 int i; 110 111 112 113 printf("origin_heapa[]="); 114 115 for(i = 0; i< 10; i++) 116 117 printf("%d ",a[i]); 118 119 printf(" "); 120 121 122 123 build_max_heap(a); 124 125 printf(" max_heap a[]="); 126 127 for(i = 0; i< 10; i++) 128 129 printf("%d ",a[i]); 130 131 printf(" "); 132 133 134 135 heapsort(a); 136 137 printf("heap_sort a[]="); 138 139 for(i = 0; i< 10; i++) 140 141 printf("%d ",a[i]); 142 143 printf(" "); 144 145 }
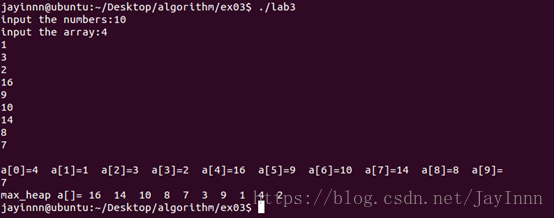
(三)用插入法建堆
1 #include <stdio.h> 2 3 #include <stdlib.h> 4 5 6 7 #define a_length 10 8 9 int a_heap_size; 10 11 int insert_length; 12 13 14 15 int parent(int i){ 16 17 int a; 18 19 a = (i-1)/2; 20 21 return a; 22 23 } 24 25 26 27 void heap_increase_key(int a[], int i, int key){ 28 29 int exchange; 30 31 int a_end; 32 33 //if(key <a[i-1]) 34 35 // printf("new key is smaller than currentkey! "); 36 37 a_end = i - 1; 38 39 a[a_end] = key; 40 41 42 43 while(a_end> 0 && a[parent(a_end)] < a[a_end]){ 44 45 exchange = a[a_end]; 46 47 a[a_end] = a[parent(a_end)]; 48 49 a[parent(a_end)]= exchange; 50 51 a_end = parent(a_end); 52 53 // printf(" 1111111111111 "); 54 55 } 56 57 } 58 59 60 61 void max_heap_insert(int a[], int key){ 62 63 a_heap_size =a_heap_size + 1; 64 65 a[a_heap_size-1]= -1; 66 67 heap_increase_key(a,a_heap_size, key); 68 69 } 70 71 72 73 void build_max_heap(int a[]){ 74 75 int i; 76 77 a_heap_size =1; 78 79 for(i = 1; i< insert_length; i++){ 80 81 max_heap_insert(a,a[i]); 82 83 // printf(" 66666666666 "); 84 85 } 86 87 } 88 89 90 91 int main(){ 92 93 inta[a_length]; 94 95 int number,i; 96 97 printf("inputthe numbers:"); 98 99 scanf("%d",&number); 100 101 //printf(" "); 102 103 //printf("number=%d ",number); 104 105 insert_length= number; 106 107 108 109 printf("inputthe array:"); 110 111 for(i = 0; i< number; i++) 112 113 scanf("%d",&a[i]); 114 115 116 117 printf(" "); 118 119 for(i = 0; i <number; i++) 120 121 printf("a[%d]=%d ",i,a[i]); 122 123 printf(" "); 124 125 126 127 build_max_heap(a); 128 129 printf("max_heapa[]= "); 130 131 for(i = 0; i< number; i++) 132 133 printf("%d ",a[i]); 134 135 printf(" "); 136 137 }