读书笔记：对抗过拟合

(本文是根据 neuralnetworksanddeeplearning 这本书的第三章Improving the way neural networks learn整理而成的读书笔记，根据个人口味做了删减)

上一章，我们学习了改善网络训练的代价函数：交叉熵函数。今天要介绍神经网络容易遇到的过拟合（overfitting）问题，以及解决的方法：正则化（regularization）。

过拟合

过拟合现象

在了解过拟合这个问题之前，我们先做个实验。

假设我们使用一个有 30 个隐藏层，23860 个参数的网络来预测 MNIST 数据集。不过，我们只用数据集中的 1000 张图片进行训练。训练过程和以往一样，代价函数采用交叉熵函数，学习率 (eta = 0.5)，batch 大小为 10，并且训练 400 轮。

下图是训练过程中 cost 的变化：

可以看到，cost 是在逐渐变小的。不过这是否意味着网络被训练得越来越好呢？我们来看看每一轮的准确率情况：

在大概 280 轮训练之前，网络的准确率确实在缓慢上升，但之后，我们看到，准确率基本没有大的改进，始终维持在 82.20 上下。这和 cost 下降的情况是背道而驰的。这种看似得到训练，其实结果很差的情况，就是过拟合（overfitting）。

出现过拟合的原因在于，网络模型的泛化能力很差。也就是说，模型对训练数据的拟合程度非常好，但对未见过的新数据，就几乎没什么拟合能力了。

要更进一步了解过拟合现象，我们再来看看其他实验。

下图是训练过程中，在测试数据上的 cost（之前是训练数据上的）：

图中，cost 在前 15 轮训练中逐渐改善，但之后却又开始上升。这是网络出现过拟合的信号之一。

另一个过拟合的信号请看下图：

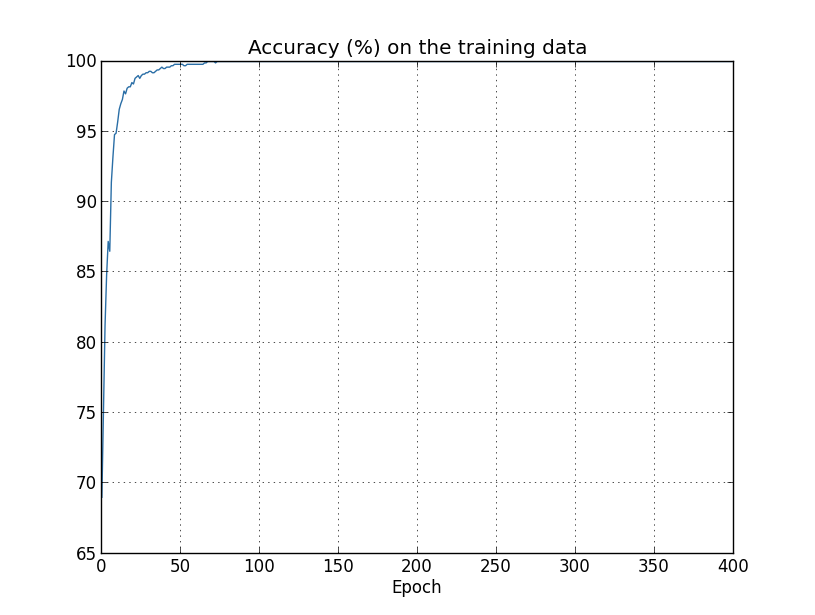
这是训练集上的准确率。可以看出，网络的准确率一路上升直到 100%。有人可能会疑惑，准确率高不是好事吗？确实，准确率高是我们需要的，但必须是测试集上的准确率。而训练集上的高准确率，带来的结果未必是好事。它可能意味着，网络在训练数据上「钻了牛角尖」。它并不是学习出如何识别手写体数字，而是仅仅记住了训练数据长什么样。换句话说，它在训练数据上拟合太过了。

过拟合在现代神经网络中是很常见的问题，因为网络参数巨大，一旦训练样本不够丰富，有些参数就可能没有训练到。为了有效地训练网络，我们需要学习能够减少过拟合的技巧。

交叉验证集

在解决过拟合这个问题上，我们需要引入另一个数据集——交叉验证集（validation dataset）。

交叉验证集可以认为是一种双保险措施。在解决过拟合时，我们会用到很多技巧，有些技巧本身就带有自己的参数（也就是我们说的超参数(hyper parameter)），如果只在测试集上试验，结果可能导致我们解决过拟合的措施有针对测试集的「嫌疑」，或者说，在测试集上过拟合了。因此，用一个新的交叉验证集来评估解决的效果，再在测试集上试验，可以让网络模型的泛化能力更强。

三个解决过拟合的小办法

之所以称为小办法，即这种方法虽然有效，但要么作用很小，要么实践意义不大。

early stop

检测过拟合有一个很明显的方法，就是跟踪测试集上的准确率。当准确率不再上升时，就停止训练（early stop）。当然，严格来讲，这不是过拟合的充要条件，可能训练集和测试集上的准确率都停止上升了。但这种策略仍然有助于缓解过拟合问题。

不过，在实践中，我们通常是跟踪验证集上的准确率，而非测试集。

增加训练数据

上图是用所有训练数据进行训练时，训练集和测试集上准确率的变化情况。

可以看出，相比之前只用 1000 个训练样本的情况，网络在训练集和测试集上的准确率只想差了 2.53%（之前是 17.73%）。也就是说，增加训练数据后，过拟合问题很大程度上缓解下来了。所以，增加训练数据也是解决过拟合的办法之一（而且是最简单有效的方法，所谓「算法好不如数据好」）。不过，增加数据不是简单地将数据拷贝复制，而是让数据的种类样式更加丰富。

在真实情况中，训练数据是很难获取的，所以这种方法实践起来很困难。

减少模型参数

减少模型参数本质上和增加训练数据是一样的，不过，对于神经网络而言，参数越多，效果一般会更好，所以这种方法不是逼不得已，我们一般不会采纳。

正则化

L2 正则化

正则化是解决过拟合常用的方法。在这一节中，我们将介绍最常用的正则化技巧：L2 正则化（weight decay）。

L2 正则化是在代价函数中添加正则化项(regularization term)。比如，下面是正则化后的交叉熵函数：

[C=-frac{1}{n}sum_{xj}{[y_j ln a_j^L+(1-y_j)ln(1-a_j^L)]}+frac{lambda}{2n}sum_w{w^2} ag{85} ]

所谓正则化项，其实就是权值的平方和，前面的 (lambda / 2n) 是针对所有样本取均值，而 (lambda) 就是我们说的超参数。之后会讨论 (lambda) 的值该如何取。注意，正则项中并没有偏差，因为对偏差的正则化效果不明显，所以一般只对权值进行正则化。

L2 正则化也可以用在其他代价函数中，比如平方差函数：

[C=frac{1}{2n}sum_x{||t-a^L||^2}+frac{lambda}{2n}sum_w{w^2} ag{86} ]

我们可以写出 L2 正则化的通式：

[egin{eqnarray} C = C_0 + frac{lambda}{2n}sum_w w^2, ag{87}end{eqnarray} ]

其中，(C_0) 是原先的代价函数。

直观上，正则化的效果就是让学习的权值尽可能的小。可以说，正则化就是在最小化原代价函数和寻找小权值之间找折中。而两者之间的重要性由 (lambda) 控制。当 (lambda) 大时，网络会尽可能减小权重，反之，则尽可能减小原先的代价函数。

我们先通过一些实验看看这种正则化的效果。

添加正则化项后，梯度下降的偏导数会发生一点变化：

[egin{eqnarray} frac{partial C}{partial w} & = & frac{partial C_0}{partial w} + frac{lambda}{n} w ag{88}\ frac{partial C}{partial b} & = & frac{partial C_0}{partial b}. ag{89}end{eqnarray} ]

其中，(partial C_0/partial w) 和 (partial C_0/partial b) 可以通过 BP 算法计算，因此，新的偏导数很容易计算：

[egin{eqnarray} w & ightarrow & w-eta frac{partial C_0}{partial w}-frac{eta lambda}{n} w ag{91}\ & = & left(1-frac{eta lambda}{n} ight) w -eta frac{partial C_0}{partial w}. ag{92}end{eqnarray} \ ]

[egin{eqnarray} b & ightarrow & b -eta frac{partial C_0}{partial b}. ag{90}end{eqnarray} ]

在批训练时，梯度下降公式变为：

[egin{eqnarray} w ightarrow left(1-frac{eta lambda}{n} ight) w -frac{eta}{m} sum_x frac{partial C_x}{partial w}, ag{93}end{eqnarray} ]

（注意，式子前半部分除的是训练数据大小 n，后半部分是批训练的 m）

现在，在 1000 个训练样本的例子中，我们加入正则化项（(lambda) 设为0.1，其他参数和之前一样），并看看训练的结果如何：

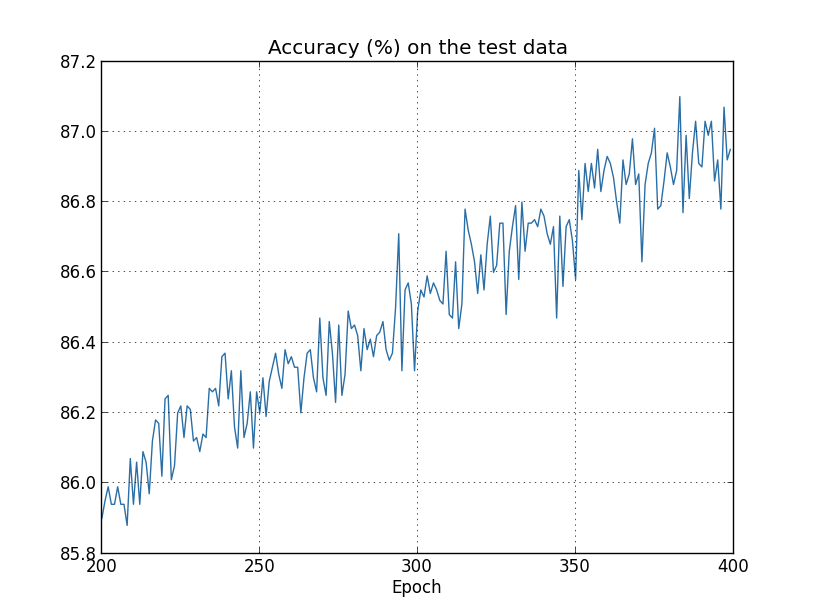
可以看出，准确率较之前的 82.27% 有了明显的提高，也就是说，正则化确实在一定程度上抑制了过拟合。

现在，我们用所有的 50000 张图片训练，看看正则化能否起作用（这里我们设置 (lambda) 为 5.0，因为 n 由原来的 1000 变为 50000，如果 (lambda) 的值和之前一样，那么 (frac{eta lambda}{n}) 的值就会小很大，weight decay 的效果就会大打折扣）。

可以看到，准确率上升到 96.49%，而且测试集准确率和训练集准确率之间的差距也进一步缩小了。

为什么正则化能减小过拟合

这个问题可以用奥卡姆剃刀(Occam's Razor)来解释。奥卡姆剃刀的思想是，如果两个模型都能拟合数据，那么我们优先选择简单的模型。

正则化给神经网络带来的影响是：权值 (绝对值) 会更小。权值小的好处是，当输入发生微小的变化时，网络的结果不会发生大的波动，相反地，如果权值 (绝对值) 过大，那么一点点变化也会产生很大的响应（包括噪声）。从这一点来看，我们可以认为正则化的网络是比较简单的模型。

当然，简单的模型也未必是真正有用的，更关键的是要看模型的泛化能力是否足够好。关于正则化，人们一直没法找出系统科学的解释。由于神经网络中，正则化的效果往往不错，因此大部分情况下，我们都会对网络进行正则化。

其他正则化技巧

L1 正则化

L1 正则化的形式和 L2 很像，只不过正则化项略有区别：

[C=C_0+frac{lambda}{n}sum_w{|w|} ag{95} ]

下面来看看 L1 正则化对网络产生的影响。

首先，我们对 (95) 式求偏导：

[egin{eqnarray} frac{partial C}{partial w} = frac{partial C_0}{partial w} + frac{lambda}{n} \, { m sgn}(w), ag{96}end{eqnarray} ]

其中，({ m sgn}(w)) 表示 (w) 的符号，如果 (w) 为正，则为 +1，否则为 -1。

这样，梯度下降的公式就变成：

[w ightarrow w'=w-frac{eta lambda}{n}{ m sgn}(w)-eta frac{partial C_0}{partial w} ag{97} ]

对比 L2 的公式 (93)，我们发现，两个式子都有缩小 weight 的功能，这跟之前分析正则化能起作用的原因是一致的。只不过 weight 缩小的方式不一样。在 L1 中，正则化项让 weight 以一个固定的常数向 0 靠近（weight 是正是负都一样），而 L2 中weight 减小的量跟 weight 本身存在一个比例关系（也就是说，weight 越小，这个量也越小）。所以，当 weight 的绝对值很大时，L2 对 weight 的抑制作用比 L1 大。

在上式中，存在一个缺陷：当 (w=0) 时，(|w|) 是没法求导的。这个时候，我们只需要简单地令 ({ m sgn}(w)=0) 即可。

dropout

dropout 和 L1、L2 存在很大区别，它不会修改代价函数，相反地，它修改的是网络的结构。

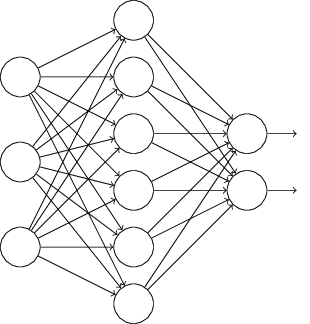
假设我们要训练如下的网络：

在梯度下降时，dropout 会随机删除隐藏层中一半的神经元，如下（虚线表示删除的神经元）：

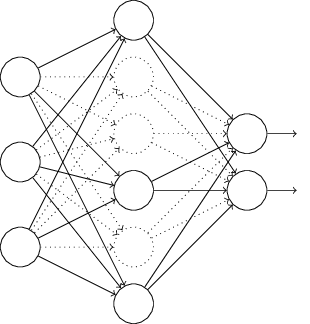
让网络在这种「残缺」的状态下训练。

当开始下一轮 batch 训练时，我们先恢复完整的网络，然后继续随机删除隐藏层中一半的神经元，再训练网络。如此循环直到训练结束。

当要使用网络预测的时候，我们会恢复所有的神经元。由于训练时只有一半的神经元启动，因此每个神经元的权值等价于完整网络的两倍，所以，真正使用网络预测时，我们要取隐藏层的权值的一半。

dropout 的思想可以这么理解：假设我们按照标准模式 (没有 dropout) 训练很多相同结构的网络，由于每个网络的初始化不同，训练时的批训练数据也会存在差异，因此每个网络的输出都会存在差别。最后我们取所有网络的结果的均值作为最终结果（类似随机森林的投票机制）。例如，我们训练了 5 个网络，有 3 个网络将数字分类为「3」，那么我们就可以认为结果是「3」，因为另外两个网络可能出错了。这种平均的策略很强大，因为不同的网络可能在不同程度上出现了过拟合，而平均取值可以缓解一定程度的过拟合现象。dropout 每次训练时会 drop 一些神经元，这就像在训练不同的网络，dropout 的过程就像在平均很多网络的结果，因此最终起到减小 overfitfing 的作用。

人工扩展训练数据

除了 dropout，扩展训练数据也是缓解过拟合的有效策略。

为了解训练数据集对结果的影响，我们准备做几组实验。每组实验的训练集大小不同，训练的轮数和正则化的参数 (lambda) 也会做相应调整，其他参数则保持不变。

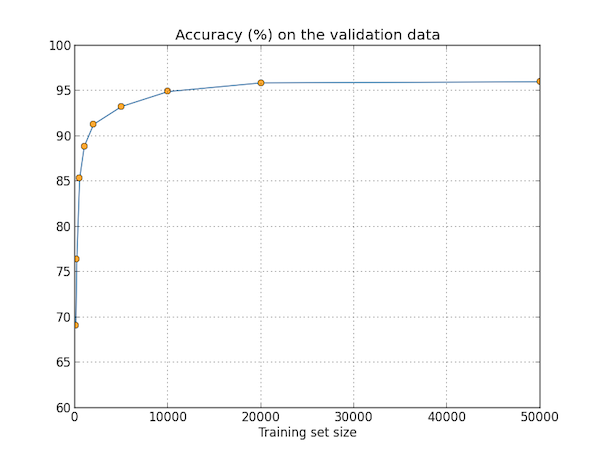
正如图中所示，训练数据量的增加有助于提高分类的准确率。图中的结果看似网络已经趋于收敛，但换成对数坐标后，这种效果就更加明显了：

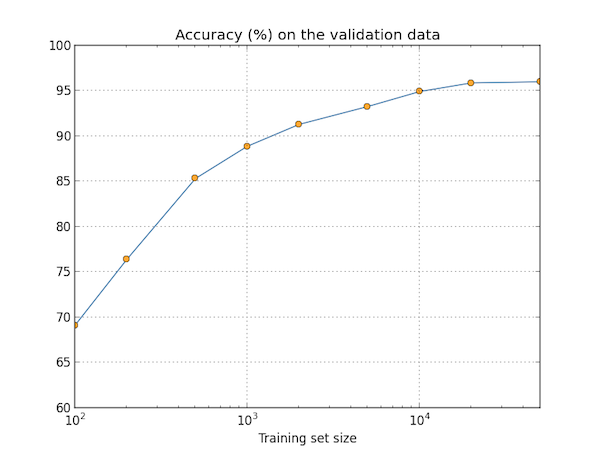
因此，如果我们能将数据集扩大到几十万几百万，准确率应当能够持续上升。

获得更多训练数据是很困难的，不过好在我们有其他技巧达到类似的作用，那就是人工扩展数据。

例如，我们有一张 MNIST 的训练图片：

旋转 15º 后，我们就得到另一张样本图片：

这两张图片肉眼都可以看出是「5」，但在像素级别上，它们差别很大，因此不失为不错的训练样本。重复这种做法（旋转平移等等操作），我们可以获得数倍于原训练数据集大小的样本。

这种做法效果明显，在很多实验中都取得成功。而且，这种思想不仅仅局限于图片识别，在其他任务（如：语音识别）中，这种做法同样奏效。

另外，数据量也可以弥补机器学习算法的不足。假设在相同数据规模下，算法 A 要好于算法 B，但如果为算法 B 提供更多数据，后者的效果往往会超过前者。而且，即使两者数据规模一样，但算法 B 的数据比 A 的更加丰富，B 也可能超过 A，这就是所谓好的算法不如好的数据。

参考

• Improving the way neural networks learn