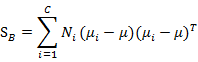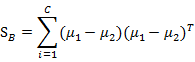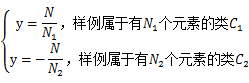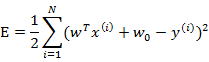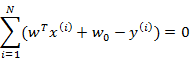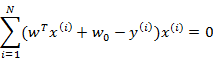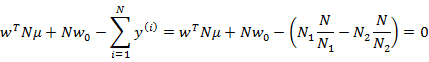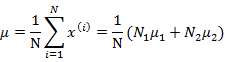4. 实例
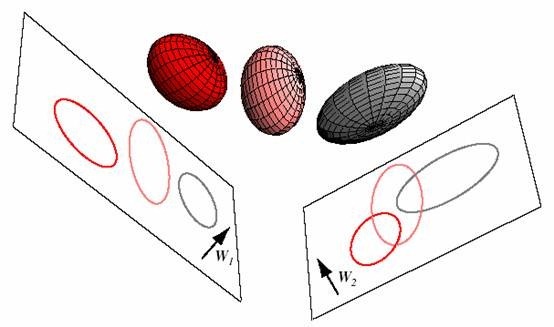
将3维空间上的球体样本点投影到二维上,W1相比W2能够获得更好的分离效果。
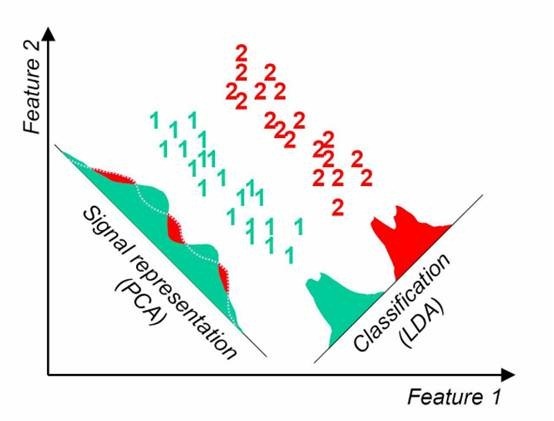
PCA与LDA的降维对比:
PCA选择样本点投影具有最大方差的方向,LDA选择分类性能最好的方向。
LDA既然叫做线性判别分析,应该具有一定的预测功能,比如新来一个样例x,如何确定其类别?
拿二值分来来说,我们可以将其投影到直线上,得到y,然后看看y是否在超过某个阈值y0,超过是某一类,否则是另一类。而怎么寻找这个y0呢?
看
根据中心极限定理,独立同分布的随机变量和符合高斯分布,然后利用极大似然估计求
然后用决策理论里的公式来寻找最佳的y0,详情请参阅PRML。
这是一种可行但比较繁琐的选取方法,可以看第7节(一些问题)来得到简单的答案。
5. 使用LDA的一些限制
1、 LDA至多可生成C-1维子空间
LDA降维后的维度区间在[1,C-1],与原始特征数n无关,对于二值分类,最多投影到1维。
2、 LDA不适合对非高斯分布样本进行降维。
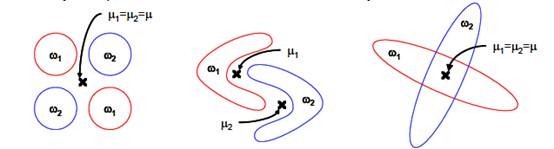
上图中红色区域表示一类样本,蓝色区域表示另一类,由于是2类,所以最多投影到1维上。不管在直线上怎么投影,都难使红色点和蓝色点内部凝聚,类间分离。
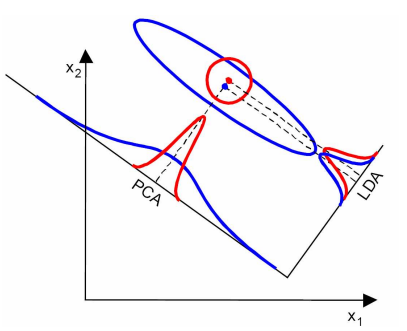
3、 LDA在样本分类信息依赖方差而不是均值时,效果不好。
上图中,样本点依靠方差信息进行分类,而不是均值信息。LDA不能够进行有效分类,因为LDA过度依靠均值信息。
4、 LDA可能过度拟合数据。
6. LDA的一些变种
1、 非参数LDA
非参数LDA使用本地信息和K临近样本点来计算![]() ,使得
,使得![]() 是全秩的,这样我们可以抽取多余C-1个特征向量。而且投影后分离效果更好。
是全秩的,这样我们可以抽取多余C-1个特征向量。而且投影后分离效果更好。
2、 正交LDA
先找到最佳的特征向量,然后找与这个特征向量正交且最大化fisher条件的向量。这种方法也能摆脱C-1的限制。
3、 一般化LDA
引入了贝叶斯风险等理论
4、 核函数LDA
7. 一些问题
上面在多值分类中使用的
是带权重的各类样本中心到全样本中心的散列矩阵。如果C=2(也就是二值分类时)套用这个公式,不能够得出在二值分类中使用的![]() 。
。
对于二值分类问题,令人惊奇的是最小二乘法和Fisher线性判别分析是一致的。
下面我们证明这个结论,并且给出第4节提出的y0值得选取问题。
回顾之前的线性回归,给定N个d维特征的训练样例![]() (i从1到N),每个
(i从1到N),每个![]() 对应一个类标签
对应一个类标签![]() 。我们之前令y=0表示一类,y=1表示另一类,现在我们为了证明最小二乘法和LDA的关系,我们需要做一些改变
。我们之前令y=0表示一类,y=1表示另一类,现在我们为了证明最小二乘法和LDA的关系,我们需要做一些改变
就是将0/1做了值替换。
我们列出最小二乘法公式
从第一个式子展开可以得到
消元后,得
可以证明第二个式子展开后和下面的公式等价
因此,最后结果仍然是
这个过程从几何意义上去理解也就是变形后的线性回归(将类标签重新定义),线性回归后的直线方向就是二值分类中LDA求得的直线方向w。
好了,我们从改变后的y的定义可以看出y>0属于类![]() ,y<0属于类
,y<0属于类![]() 。因此我们可以选取y0=0,即如果
。因此我们可以选取y0=0,即如果![]() ,就是类
,就是类![]() ,否则是类
,否则是类![]() 。
。
写了好多,挺杂的,还有个topic模型也叫做LDA,不过名字叫做Latent Dirichlet Allocation,第二作者就是Andrew Ng大牛,最后一个他导师Jordan泰斗了,什么时候拜读后再写篇总结发上来吧。