数据结构C语言实现----树

树的基本知识点

　　树的定义

　　树的ADT（抽象数据类型）

　　树的储存结构

　　二叉树的定义

　　二叉树的储存结构

　　遍历二叉树

　　二叉树的建立

二叉树的ADT

　　

typedef struct BiTNode
{
    ElemType date;        //结点的数据域
    struct BiTNode *lchild , *rchild;        //指向左孩子，右孩子
} BiTNode ,  *BiTree;

　　其中 BiTNode T  等价于  BiTNode *T

二叉树的遍历

　　有三种遍历方式：(V是访问visist  ， L是左边left  ，R是右边right）（先访问根节点就叫先序，中间访问根节点就叫中序）

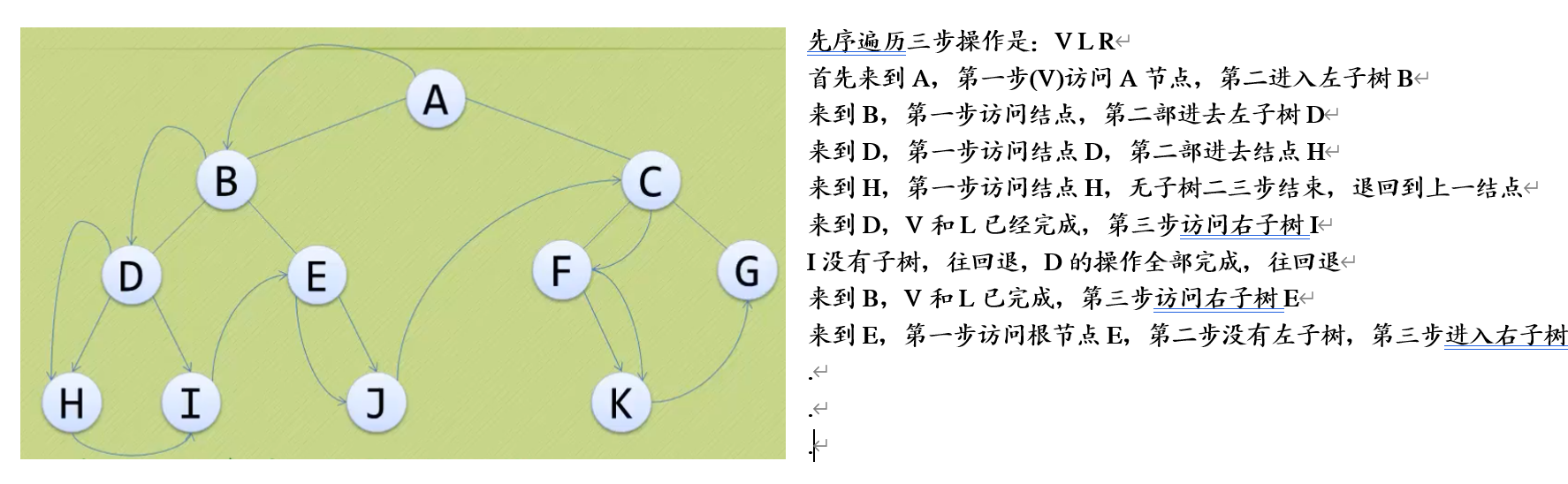
　　　　VLR（先序）:先访问根结点，再先序遍历左子树，再先序遍历右子树（后面有举例）

　　　　LVR（中序）:先中序遍历左子树，再访问根节点，再中序遍历右子树

　　　　LRV（后序）:先后序遍历左子树，再后序遍历右子树，再访问根节点

遍历实例举例：

　　每进去一个新节点都要操作三个步骤：V或L或R　　

　　（1）先序遍历

　　

void PreOrdeTraverse(BiTree T)
{
    if (T)
    {//递归结束条件，T*为空
        visit(T->date);    //访问根节点
        PreOrdeTraverse(T->lchild);    //先序遍历左子树
        PreOrdeTraverse(T->rchild);    //先序遍历右子树
    }
}

　　

　　（2)中序遍历

　　中序遍历的方法与先序遍历一样，只不过顺序有改变，每当来到一个新节点，先看有没有左子树，有左子树，就进去左子树，没有就访问当前结点，之后再去找右子树，没有左右子树或左右子树结点都访问了，就回到上一个结点

　　

void InOrdeTraverse(BiTree T)
{
    if (T)
    {
        InOrdeTraverse(T->lchild);
        visit(T->date);
        InOrdeTraverse(T->rchild);
    }
}

　　(3)后序遍历

　　

void PosOrdeTraverse(BiTree T)
{
    if (T)
    {
        PosOrdeTraverse(T->lchild);
        PosOrdeTraverse(T->rchild);
        visit(T->date);
    }
}

　　

二叉树的建立

　　

//先序序列创建一颗二叉树
void CreatBiTree(BiTree *T)
{
    char c;
    scanf("%c" , &c);
    if (c == '#')  *T = NULL;
    else
    {
        *T = (BiTNode*)malloc(sizeof(BiTNode));     //给结点申请一个空间
        (*T)->date = c;
        CreatBiTree(&((*T)->lchild));       //创建左子树
        CreatBiTree(&((*T)->rchild));       //创建右子树
    }
}

　　

　　这里说明一下，为什么要传入树的指针的指针

　　假如我们要用一个函数去改变一个整型变量 n 的值 ，我们知道必须传入这个变量n的指针进去这个函数，要不然函数中n的变化影响不了函数外的n值

　　这里也是一样，我们要改变左右子树的地址，让他们指向一个新的空间，所以要传入左右子树地址的地址，才能在函数里改变他们的地址

　　

实例：

　　　　　以先序序列输入一棵树，并用三种遍历方式打印出这棵树，并且找到某个字母所在的层数

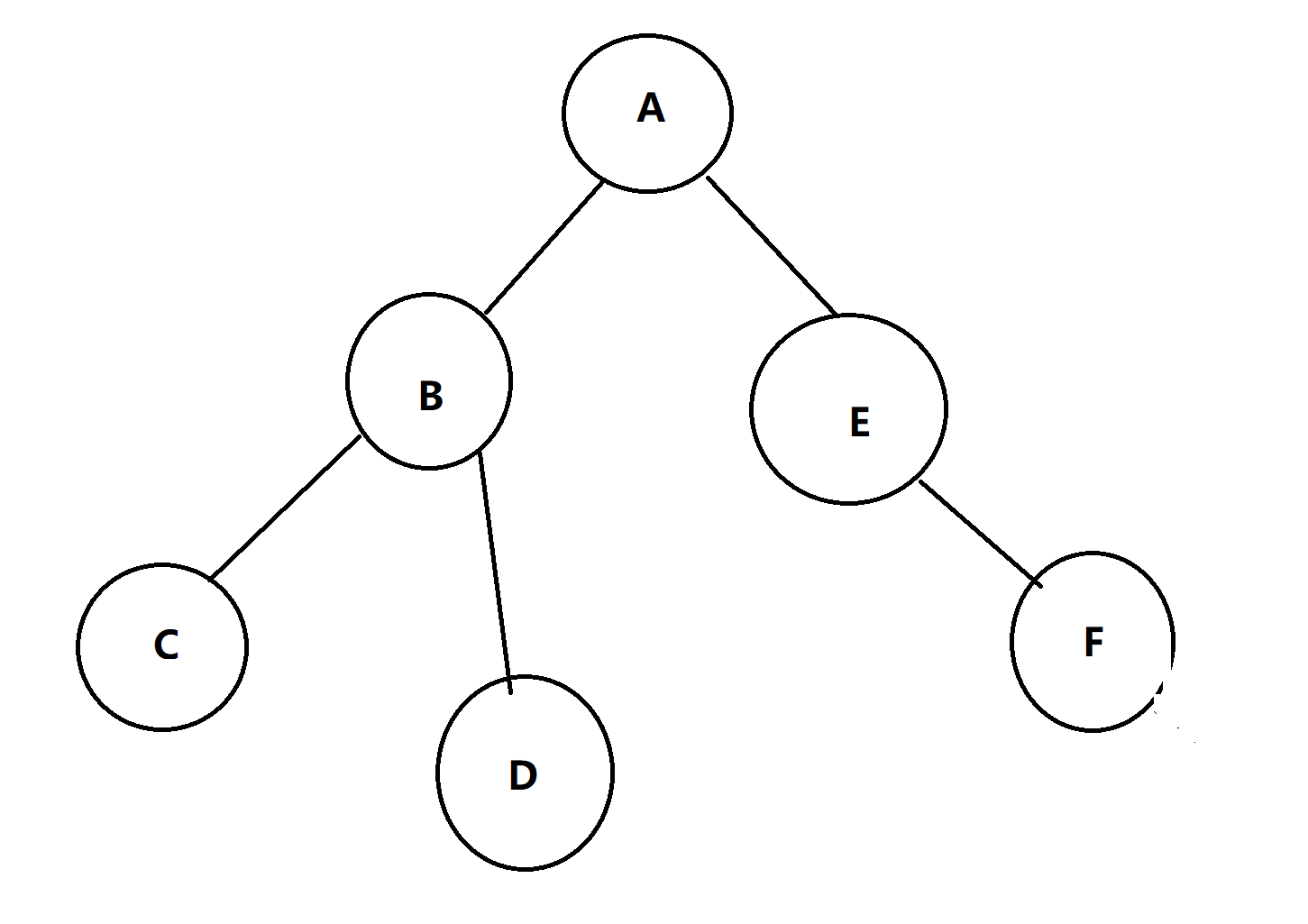
　　　　　我们下面这棵树为例（没有子树记作#）（找到大写字母D的所在层数）

　　　　　

#include<stdio.h>
#include<stdlib.h>

typedef struct BiTNode
{
    char date;         //结点的数据域
    struct BiTNode *lchild , *rchild;       //指向左孩子和右孩子
}BiTNode , *BiTree ;
//先序序列创建一颗二叉树
void CreatBiTree(BiTree *T)
{
    char c;
    scanf("%c" , &c);
    if (c == '#')  *T = NULL;
    else
    {
        *T = (BiTNode*)malloc(sizeof(BiTNode));     //给结点申请一个空间
        (*T)->date = c;
        CreatBiTree(&((*T)->lchild));       //创建左子树
        CreatBiTree(&((*T)->rchild));       //创建右子树
    }
}
//访问二叉树结点操作
void visit(char c)
{
    printf("%c",c);
}
//先序遍历二叉树
void PreOrdeTraverse(BiTree T)
{
    if (T)
    {
        visit(T->date);
        PreOrdeTraverse(T->lchild);
        PreOrdeTraverse(T->rchild);
    }
    
}
//中序遍历二叉树
void InOrdeTraverse(BiTree T)
{
    if (T)
    {
        InOrdeTraverse(T->lchild);
        visit(T->date);
        InOrdeTraverse(T->rchild);
    }
}
//后序遍历二叉树
void PosOrdeTraverse(BiTree T)
{
    if (T)
    {
        PosOrdeTraverse(T->lchild);
        PosOrdeTraverse(T->rchild);
        visit(T->date);
    }
}
//查找字母D在第几层
void serch(BiTree T , int leavel)
{
    if (T){
        if (T->date == 'D')
        {
            printf("D在第%d层！",leavel);
        }
        serch(T->lchild , leavel+1);
        serch(T->rchild , leavel+1);
    }
}
int main()
{
    BiTree T;
    int leavel = 1;
    printf("请输入先序创建的二叉树，以#结束：");
    CreatBiTree(&T);
    printf("正在先序打印二叉树：");
    PreOrdeTraverse(T);
    putchar('
');
    printf("正在中序打印二叉树：");
    InOrdeTraverse(T);
    putchar('
');
    printf("正在后序打印二叉树：");
    PosOrdeTraverse(T);
    putchar('
');
    serch(T , leavel);
}

　　

运行结果：