k-center问题-学习

k-center问题：

In graph theory, the metric k-center or metric facility location problem is a combinatorial optimization problem studied in theoretical computer science. Given n cities with specified distances, one wants to build k warehouses in different cities and minimize the maximum distance of a city to a warehouse. In graph theory this means finding a set of k vertices for which the largest distance of any point to its closest vertex in the k-set is minimum. The vertices must be in a metric space, providing a complete graph that satisfies the triangle inequality.

complete graph：

 

G7, a complete graph with 7 vertices

 

The k-Center Clustering problem can also be defined on a complete undirected graph G = (V, E) as follows:

Given a complete undirected graph G = (V, E) with distances d(v_i, v_j) ∈ N satisfying the triangle inequality, find a subset C ⊆ V with |C| = k while minimizing:

 

In a complete undirected graph G = (V, E), if we sort the edges in nondecreasing order of the distances: d(e₁) ≤ d(e₂) ≤ … ≤ d(e_m) and let G_i = (V, E_i), where E_i = {e₁, e₂, …, e_i}. The k-center problem is equivalent to finding the smallest index i such that G_i has a dominating set of size at most k.

Dominating set：

In graph theory, a dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is adjacent to at least one member of D. The domination number γ(G) is the number of vertices in a smallest dominating set for G.

 

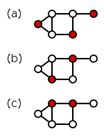
Dominating sets (red vertices)

The dominating set problem concerns testing whether γ(G) ≤ K for a given graph G and input K; it is a classical NP-complete decision problem in computational complexity theory.Therefore it is believed that there may be no efficient algorithm that finds a smallest dominating set for all graphs, although there are efficient approximation algorithms, as well as both efficient and exact algorithms for certain graph classes.

Figures (a)–(c) on the right show three examples of dominating sets for a graph. In each example, each white vertex is adjacent to at least one red vertex, and it is said that the white vertex is dominated by the red vertex. The domination number of this graph is 2: the examples (b) and (c) show that there is a dominating set with 2 vertices, and it can be checked that there is no dominating set with only 1 vertex for this graph.

For Dominator in control flow graphs, see Dominator (graph theory).

来源于网络