Codeforces Round #367 (Div. 2) D. Vasiliy's Multiset trie树

D. Vasiliy's Multiset

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Author has gone out of the stories about Vasiliy, so here is just a formal task description.

You are given q queries and a multiset A, initially containing only integer 0. There are three types of queries:

1. "+ x" — add integer x to multiset A.
2. "- x" — erase one occurrence of integer x from multiset A. It's guaranteed that at least one x is present in the multiset A before this query.
3. "? x" — you are given integer x and need to compute the value 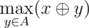, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.

Multiset is a set, where equal elements are allowed.

Input

The first line of the input contains a single integer q (1 ≤ q ≤ 200 000) — the number of queries Vasiliy has to perform.

Each of the following q lines of the input contains one of three characters '+', '-' or '?' and an integer x_i (1 ≤ x_i ≤ 10⁹). It's guaranteed that there is at least one query of the third type.

Note, that the integer 0 will always be present in the set A.

Output

For each query of the type '?' print one integer — the maximum value of bitwise exclusive OR (XOR) of integer x_i and some integer from the multiset A.

Example

Input

10
+ 8
+ 9
+ 11
+ 6
+ 1
? 3
- 8
? 3
? 8
? 11

Output

11
10
14
13

Note

After first five operations multiset A contains integers 0, 8, 9, 11, 6 and 1.

The answer for the sixth query is integer 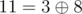 — maximum among integers 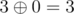, , 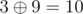, 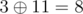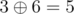and .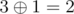

题意：n个操作，+  x表示在一个Multiset中添加一个x的数；

　　　　　　　　-  x表示在一个Multiset中删除一个x的数；

　　　　　　　　？ x表示输出x与Multiset中一个最大的异或值

思路：trie数，找x的二进制为相反，相反的位置最大结果越优；

#include<bits/stdc++.h>
using namespace std;
#define ll __int64
#define mod 1000000007
#define pi (4*atan(1.0))
const int N=1e5+10,M=4e6+10,inf=1e9+10;
int a[M][3],sum[M],len;
void init()
{
    memset(a,0,sizeof(a));
    memset(sum,0,sizeof(sum));
    len=1;
}
void insertt(int x)
{
    int num[35];
    memset(num,0,sizeof(num));
    int flag=0;
    while(x)
    {
        num[flag++]=x%2;
        x/=2;
    }
    int u=0,n=34;
    for(int i=n; i>=0; i--)
    {
        if(!a[u][num[i]])
        {
            a[u][num[i]]=len++;
        }
        u=a[u][num[i]];
        sum[u]++;
    }
}
void del(int x)
{
    int num[35];
    memset(num,0,sizeof(num));
    int flag=0;
    while(x)
    {
        num[flag++]=x%2;
        x/=2;
    }
    int u=0,n=34;
    for(int i=n; i>=0; i--)
    {
        int v=a[u][num[i]];
        sum[v]--;
        if(!sum[v])
        a[u][num[i]]=0;
        u=v;
    }
}
int getans(int x)
{
    int num[35];
    memset(num,0,sizeof(num));
    int flag=0;
    while(x)
    {
        num[flag++]=x%2;
        x/=2;
    }
    for(int i=0; i<=34; i++)
        num[i]=num[i]?0:1;
    int u=0,n=34,v,w;
    int ans=0;
    for(int i=n; i>=0; i--)
    {
        if(num[i])
        {
            v=1;
            w=0;
        }
        else
        {
            w=1;
            v=0;
        }
        if(a[u][v])
        {
            u=a[u][v];
            ans+=(1<<i);
        }
        else
        u=a[u][w];
    }
    return ans;
}
char ch[10];
int main()
{
    int x,y,z,i,t;
    int T,cas;
    init();
    insertt(0);
    scanf("%d",&T);
    for(cas=1; cas<=T; cas++)
    {
        scanf("%s %d",ch,&x);
        if(ch[0]=='+')
        insertt(x);
        else if(ch[0]=='-')
        del(x);
        else
        printf("%d
",getans(x));
    }
    return 0;
}