数论入门

声明：该讲解来自计蒜客，仅供个人学习使用

整除与带余数除法

 

最大公约数

 欧几里得算法

int gcd(int a,int b)
{
    return b? gcd(b,a%b):a;
}

质数

 

int is_prime(int n) {
    for (int i = 2; i * i <= n; ++i) {
        if (n % i == 0) {
            return 0; // 不是质数
        }
    }
    return 1; // 是质数
}

for (int i = 2; i <= n; ++i) {
    is_prime[i] = 1;
}
for (int i = 2; i <= n; ++i) {
    for (int j = i * 2; j <= n; j += i) {
        is_prime[j] = 0;
    }
}

for (int i = 2; i <= n; ++i) {
    is_prime[i] = 1;
}
for (int i = 2; i * i <= n; ++i) {
    if (is_prime[i]) {
        for (int j = i * i; j <= n; j +=i) {
             is_prime[j] = 0;
        }
    }
}

二分快速幂

int Pow_mod(int a, int b, int mod) {
    if (b == 0) {
         return 1%mod;
    }
    int temp = Pow_mod(a, b/2, mod);
    temp = temp * temp % mod;
    if (b%2 == 1) {
         temp = temp * a % mod;
    }
    return temp;
}

这样我们便得到了 O(lgb) 的时间复杂度的算法计算 a^b次方。

int Pow_mod(int a, int b, int mod){
    int res = 1, temp = a;
    for (; b; b /= 2) {
        if (b & 1) {
            res = res * temp % mod; // 2进制上这一位为1，乘上这一位权值
        }
        temp = temp * temp % mod; // 位数加1， 权值平方
    }
    return res;
}

排列组合

矩阵

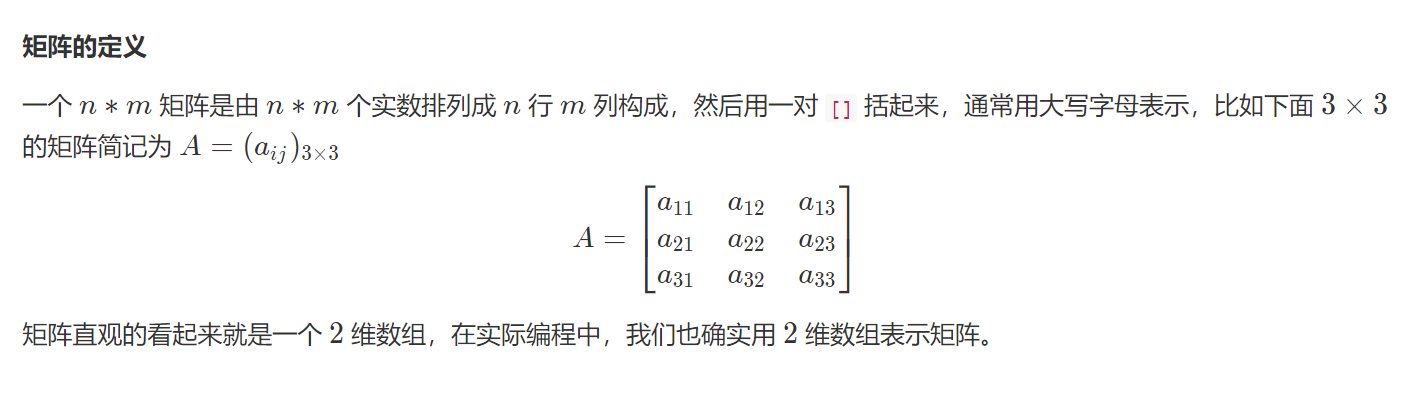
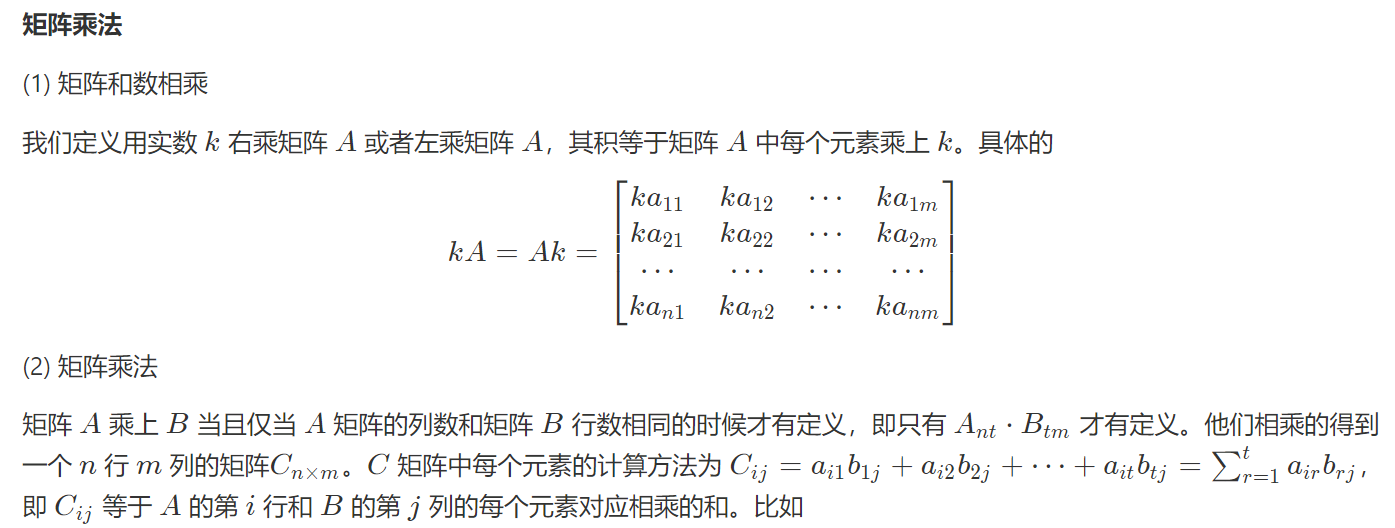
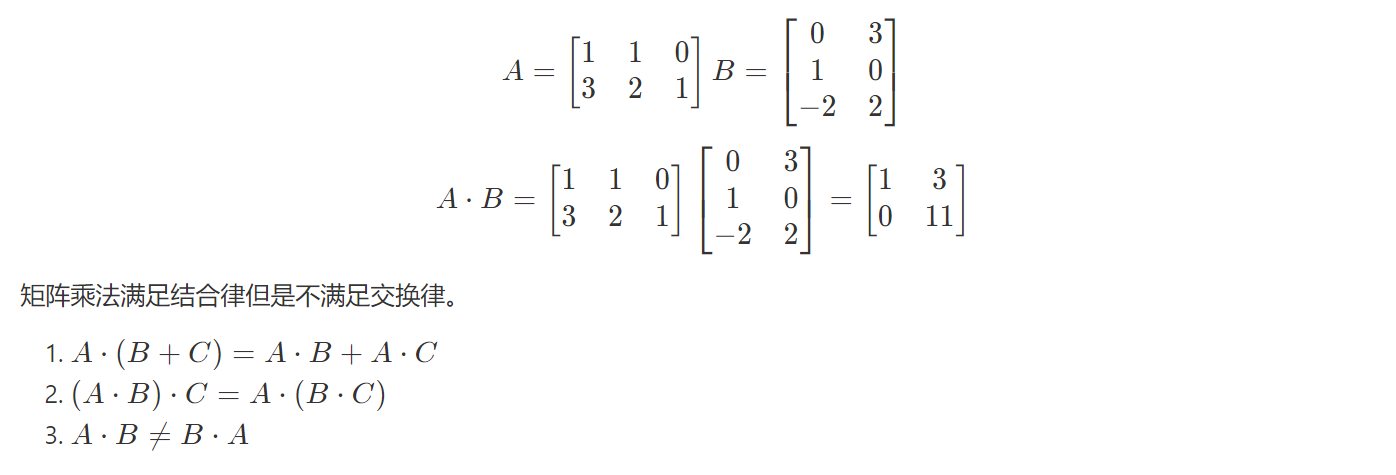
struct matrix {
   int n, m;
   int a[100][100];
};
// A.m == B.n
matrix matrix_mul(matrix A, matrix B) {
    matrix C;
    C.n = A.n;
    C.m = B.m;
    for (int i = 0; i < A.n; ++i) {
        for (int j = 0; j < B.m; ++j) {
            C.a[i][j] = 0;
            for (int k = 0; k < A.m; ++k) {
                C.a[i][j] += A.a[i][k] * B.a[k][j];
            }
        }
    }
    return C;
}

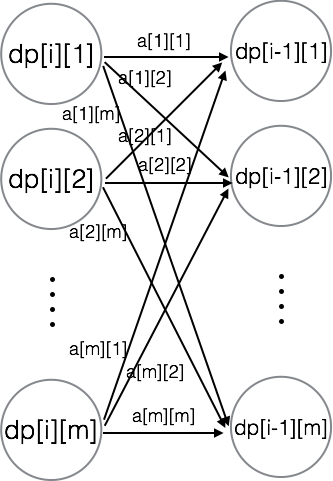
int n; // 所有矩阵都是 n * n 的矩阵
struct matrix {
   int a[100][100];
};
matrix matrix_mul(matrix A, matrix B, int mod) {
    // 2 个矩阵相乘
    matrix C;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            C.a[i][j] = 0;
            for (int k = 0; k < n; ++k) {
                C.a[i][j] += A.a[i][k] * B.a[k][j] % mod;
                C.a[i][j] %= mod;
            }
        }
    }
    return C;
}
matrix unit() {
    // 返回一个单位矩阵
    matrix res;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i == j) {
                res.a[i][j] = 1;
            } else {
                res.a[i][j] = 0;
            }
        }
    }
    return res;
}
matrix matrix_pow(matrix A, int n, int mod) {
    // 快速求矩阵 A 的 n 次方
    matrix res = unit(), temp = A;
    for (; n; n /= 2) {
        if (n & 1) {
            res = matrix_mul(res, temp, mod);
        }
        temp = matrix_mul(temp, temp, mod);
    }
    return res;
}

-