BZOJ 2666: [cqoi2012]组装

题目链接：http://www.lydsy.com:808/JudgeOnline/problem.php?id=2666

题意：n种零件，m个位置，每个位置有一种零件。求一个位置x，使得cost(1)+cost(2)+…+cost(n)最小。cost(i)表示x到最近的i类型零件的距离的平方。

思路：我们最后的最优答案一定从所有m个位置中选出了n个使得每种零件恰有一个。设第i种零件的所有位置集合是Si，Si的大小是Ci

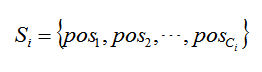
我们可以直接枚举最后选出的第i种零件是哪一个，一旦确定了这n个零件。那么最优位置是哪里呢？我们设这n个位置是x1,x2,……xn，那么

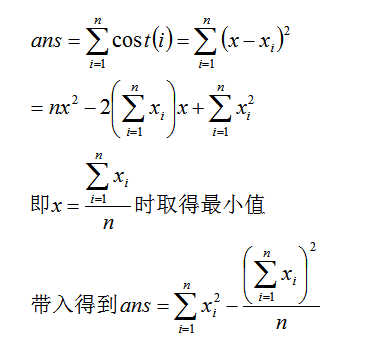
不过这样的复杂度是

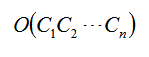
貌似有点大。我们换个思路。我们首先选取每个零件位置最小的那个，这样我们可以得到一个初始解。这个初始解很可能不是最优解。那么我们如何得到最优解？我们可以尝试每次从这个初始解中选出一个类型的零件，被该类型的另一个零件替换。那该如何选取呢？

我们将第i种类型的零件按照位置升序排序。将所有类型零件的第x个被第x+1个替换，称作一次操作，我们将所有这样的操作放在一起，每个操作用一个三元组表示：

我们将所有这些操作按照pre+next升序排序。我们下面证明：按照这个排序完的顺序依次替换一定能找到最优值。

（1）假设某一次，将某种零件的位置换了,不妨设为第一种零件，替换前的位置为A1,替换后的位置为B1。如果最优解中是B1，那么这次操作固然合理，因为我们向最优解靠近了一步；

（2）假设最优解中是A1，那么坏了，我们这样操作已经偏离了最优解。我们证明，如果到目前最优解还没找到，那么这种情况不存在，也就是最优解中不可能是A1。

假设是A1，那么也就是说在替换了其他的一些类型之后达到最优解。其他一些类型不好说，我们就假设替换了其他某一个类型后达到最优解，我们不妨设替换了第二种类型的零件，设替换前是A2，替换后是B2。在这里，我们有以下前提成立：

因为我们是准备替换第一种类型的。按照我们排序的标准有以上式子成立。

由于最后答案中的最优解是A1，而不是B1，那么有以下成立：令$X=sum_{i=3}^{n}A_{i}^{2},Y=sum_{i=3}^{n}A_{i}$

$(A_{1}^{2}+B_{2}^{2}+X)-frac{(A_{1}+B_{2}+Y)^{2}}{n}<(B_{1}^{2}+B_{2}^{2}+X)-frac{(B_{1}+B_{2}+Y)^{2}}{n}$

化简得到$A_{1}+B_{1}>frac{A_{1}+B_{1}+2B_{2}+2Y}{n}$

同理B2优于A2，那么有

$(A_{1}^{2}+B_{2}^{2}+X)-frac{(A_{1}+B_{2}+Y)^{2}}{n}leq (A_{1}^{2}+A_{2}^{2}+X)-frac{(A_{1}+A_{2}+Y)^{2}}{n}$

化简得到$A_{2}+B_{2}leq frac{A_{2}+B_{2}+2A_{1}+2Y}{n}$

 由于$(A_{1}+B_{1}+2B_{2}+2Y)-(A_{2}+B_{2}+2A_{1}+2Y)=(B_{1}+B_{2})-(A_{1}+A_{2})>0$,所以$A_{2}+B_{2}leq frac{A_{2}+B_{2}+2A_{1}+2Y}{n}<frac{A_{1}+B_{1}+2B_{2}+2Y}{n}<A_{1}+B_{1}$

即$A_{2}+B_{2}<A_{1}+B_{1}$

与前提矛盾。因此这种情况不存在。

因此我们得到算法：

const int N=100005;

int n,m;
vector<int> V[N];

struct node
{
    int x1,x2,x;

    node(int _x1=0,int _x2=0,int _x=0)
    {
        x1=_x1;
        x2=_x2;
        x=_x;
    }
};

vector<node> A;

int cmp(node a,node b)
{
    return a.x<b.x;
}

int main()
{
    n=myInt();
    m=myInt();

    for(int i=1;i<=m;i++)
    {
        int x=myInt();
        int y=myInt();
        V[y].pb(x);
    }
    double S=0,P=0;
    for(int i=1;i<=n;i++)
    {
        S+=V[i][0];
        P+=sqr(V[i][0]);
        for(int j=1;j<SZ(V[i]);j++)
        {
            A.pb(node(V[i][j-1],V[i][j],V[i][j-1]+V[i][j]));
        }
    }
    sort(A.begin(),A.end(),cmp);


    double Min=P-S*S/n,ans=S/n;

    for(int i=0;i<SZ(A);i++)
    {
        double x1=A[i].x1;
        double x2=A[i].x2;
        P-=x1*x1;
        P+=x2*x2;
        S-=x1;
        S+=x2;

        if(P-S*S/n<Min) Min=P-S*S/n,ans=S/n;
    }
    printf("%.4lf
",ans);
}