问题:求图中点1到其他各点的最短距离
策略:
1.把起点1放入初始集合Set中,从剩余的点中,选取到Set(此时Set中只有1个点)距离最近的点,并入集合Set中,
2.从剩余的点中,找经过集合Set,到起点1的最短距离,将最短边并入Set集合
3.依次循环,直到所有的边都并入Set

变量的命名:
Set={1,2,,,,,,x} //已找到start(本例中是1点)到1,2,,,,,x的最短路径的点的集合Set
dist[u]: //从start点开始,经过Set中的点,到u点的最短距离
short[u]: //从start开始到u的全局最短路径(不一定经过Set中的点)
可知short[u] <= dist[u]
证明过程:
命题:算法进行到第k步时,Set中的每个节点Set_i的dist[Set_i]等于全局最短路径short[Set_i]
(第n步时,dist[n]=short[n],此时找到点1到所有点的最短距离)
归纳基础:
k=1,Set={start_point} => dist[start_point] == short[start_point] ==0,命题正确
归纳假设:
第k步成立,则第k+1步成立
设k+1步选择了顶点v(v是剩余集合中,经过Set到start_point距离最近的点)
该顶点与Set中的u点相连, 欲证dist[v] == short[v]
反证法:假设命题不正确,即:存在start_point到点v的更短路径 L(绿色部分)为最短路径short[v],
该路径经过集合中的最后一个点为last_point,经过未收录集合的点集 uncollected_point_set中的,任1个或者多个点到达v.
本例以单点y为例,多点同理:(v和last_point不可能直接相连,若直接相连,因为dist[v]最后一点经过u,且为最短,此时L必然>=dist[v],不是更短路径)
此时 L == dist[y] + distance[y, v] == short[v]
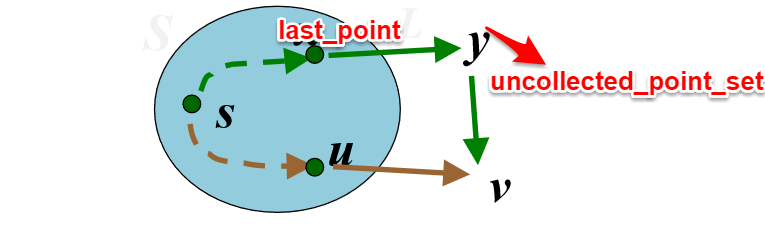
由题意知,dist[v] <= dist[y]
=>
dist[v] <= L == short[v]
dist[v]是相对于L更短的路径=>假设不成立,不存在更短的路径L为全局最短路径,第k+1步选择的点即为全局最短路
=>
命题成立!