1,概述
在NLP中孪生网络基本是用来计算句子间的语义相似度的。其结构如下
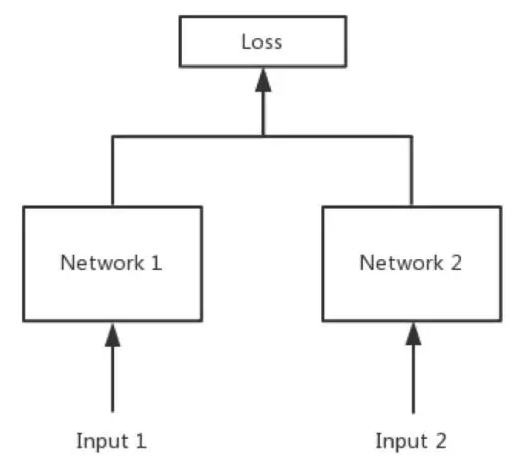
在计算句子语义相似度的时候,都是以句子对的形式输入到网络中,孪生网络就是定义两个网络结构分别来表征句子对中的句子,然后通过曼哈顿距离,欧式距离,余弦相似度等来度量两个句子之间的空间相似度。
孪生网络又可以分为孪生网络和伪孪生网络,这两者的定义:
孪生网络:两个网络结构相同且共享参数,当两个句子来自统一领域且在结构上有很大的相似度时选择该模型;
伪孪生网络:两个网络结构相同但不共享参数,或者两个网络结构不同,当两个句子结构上不同,或者来自不同的领域,或者时句子和图片之间的相似度计算时选择该模型;
另外孪生网络的损失函数一般选择Contrastive loss Function(对比损失函数)。接下来具体看看孪生网络在句子语义相似度计算中的几篇论文:
2,论文模型介绍
1)Siamese CBOW: Optimizing Word Embeddings for Sentence Representations
该论文提出了一种基于孪生网络+CBOW的方式来无监督式的训练句子的向量表示。网络的结构图如下:
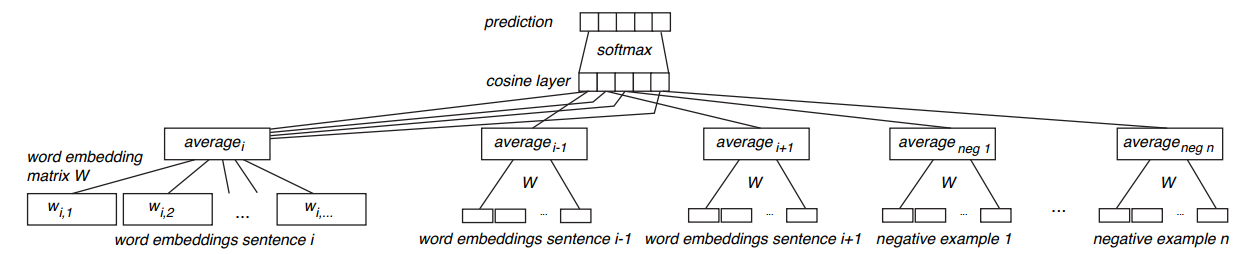
首先给定一个很大的语料库,语料库中的句子要保持原来文章中的顺序,那我们该怎么将这个无监督的任务构造成有监督式的任务呢?看论文中这个CBOW,其实就是采用了类似word2vec中的CBOW的形式来构造有监督式的任务的。我们给定一个中心句子$s_i$,然后将中心句子的上下句作为正样本(即和中心句子相关的句子),然后从其他句子中随机选择$n$个句子作为负样本,以论文中为例,负样本也选择2个。因此就构造成了这样一个句子集合$[s_i, s_{i+1}^+, s_{i-1}^+, s_1^-, s_2^-]$,那么这样一个句子集合就作为一个样本输入到模型中,以这里的例子为例,就构造成了一个具有5个相同结构相同参数的网络来处理这5个句子。有了样本之后,标签该怎么定义呢?在这里的真实标签定义如下:
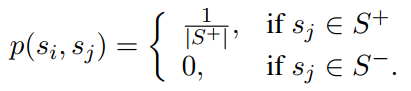
上面式子中的$S^+, S^-$分别表示正样本句子集合和负样本句子集合。因此真实标签是服从概率分布的。接下来我们看看预测标签该怎么定义,其定义如下:
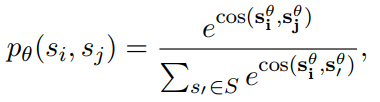
上面式子为预测标签的概率分布(softmax后的结果),其中$s_i^{ heta}$是句子$s_i$的向量表示,那么问题来了,这个句子向量是怎么得到的呢?其实模型的输入最小粒度是词,在这里会用一个词嵌入矩阵(词向量)来将每个词映射到低维向量,然后对句子中的词向量取平均来表示句子的向量。之后再计算中心句子$s_i$和其他句子的余弦相似度,然后经过softmax得到预测的概率分布。既然真实标签和预测标签都服从概率分布,那么损失函数就可以直接用交叉熵了,因此损失函数如下:

其实这里整个模型被训练的参数只有一开始的词嵌入矩阵,也就是说我们这个模型最终训练的到的也就是一个词向量,但因为目标任务是计算句子的相似度,而且损失函数的构造也是来建模句子之间的关系,因此个人人为这种方式获得的词向量,通过取平均的方式能更好的表示句子向量。因此在句子相似度的任务上的效果也是优于word2vec词向量的。
2)Siamese Recurrent Architectures for Learning Sentence Similarity
上面介绍了一种无监督的方式,接下来的模型都是有监督的。 本论文提出了一种MaLSTM的网络结构,其网络结构如下:
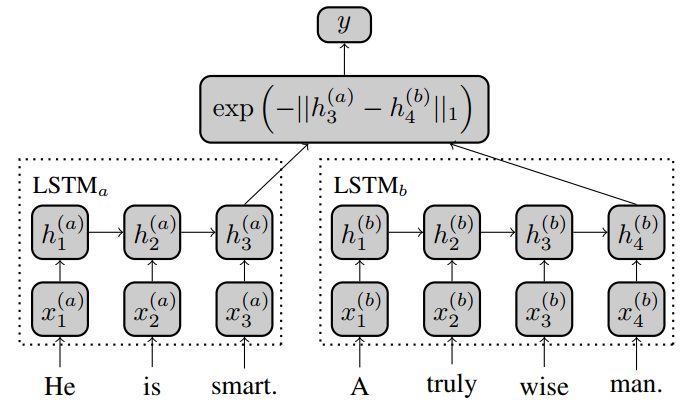
其实网络结构是并没什么新意,其具体如下:
1)通过两个LSTM网络(可以是孪生网络,也可以是伪孪生网络)来处理句子对,取LSTM最后时刻的输入作为两个句子的向量表示。
2)用曼哈顿距离来度量两个句子的空间相似度。
论文中没有提到用了什么损失函数,但一般孪生网络的损失函数都是Contrastive loss function。这个我们在下面再介绍,至于在这里作者为什么选择曼哈顿距离,作者认为欧式距离容易出现梯度消失。而且在实验中显示效果也是优于余弦相似度的,对于这个度量选择,个人认为还是以自己的实际项目来选择,并不存在一个绝对的好坏。
3)Learning Text Similarity with Siamese Recurrent Networks
该论文同样是用LSTM来处理句子对,其网络结构如下:

在这里将句子对的关系看作是一个二分类的问题,给定一个样本$[x_1, x_2, y]$,在这里$y$的结果为$[0, 1]$,因此可以看作一个二分类问题,在这里的度量方式选择的是余弦相似度,其表达式如下:
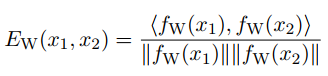
损失函数用了Contrastive loss function,其表达式如下:

从损失函数的形式上看类似于二元交叉熵损失函数,但是这里的$L_-$并不等于$1 - L_+$,其表达式如下:

其表示图如下:
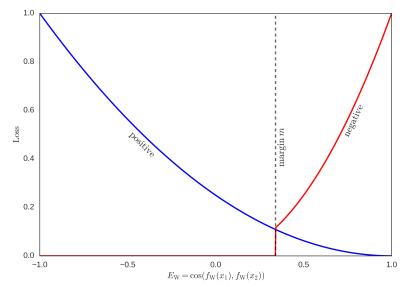
注:从这里的图来看,上面的式子是有误的,$ E_W < m$ 应该改成$E_W > m$。
我们来分析下上面的式子:假设现在是一个正样本,也就是$y^{(i)} = 1$,此时若预测的$E_W$接近于1(即预测两个句子很相似),则整体损失很小,此时若预测的$E_W$接近于-1(即预测两个句子不相似),则整体损失很大。假设现在是一个负样本,给定$m = 0.5$,也就是$y^{(i)} = 0$,此时若预测的$E_W$小于$m$,则损失为0,若预测的$E_W$大于$m$,则损失很大。其实这个损失函数可以认为通过调整$m$的值,可以控制对句子相似度的苛刻度,$m$的值比较大时,会导致两个相似的句子的余弦相似度值是比较高的。
参考文献:
Siamese CBOW: Optimizing Word Embeddings for Sentence Representations
Siamese Recurrent Architectures for Learning Sentence Similarity
Learning Text Similarity with Siamese Recurrent Networks