实验目的
用Matlab实现非线性方程的二分法、不动点迭代法
实验要求
1. 给出二分法算法和不动点迭代算法
2. 用Matlab实现二分法
3. 用Matlab实现不动点迭代法
实验内容
(1)在区间[0,1]上用二分法和不动点迭代法求 的根到小数点后六位。
的根到小数点后六位。
(2)二分法的基本思想:逐步二分区间[a,b],通过判断两端点函数值的符号,进一步缩小有限区间,将有根区间的长度缩小到充分小,从而,求得满足精度要求的根的近似值。
(3)不动点迭代法基本思想:已知一个近似根,构造一个递推关系(迭代格式),使用这个迭代格式反复校正根的近似值,计算出方程的一个根的近似值序列,使之逐步精确法,直到满足精度要求(该序列收敛于方程的根)。
实验步骤
(1)二分法算法与MATLAB程序(二分法的依据是根的存在性定理,更深地说是介值定理)。


MATLAB程序,

1 %二分法 2 %输入:f(x)=0的f(x),[a,b]的a,b,精度ep 3 %输出:近似根root,迭代次数k 4 function [root,k]=bisect(fun,a,b,ep) 5 if nargin>3 6 elseif nargin<4 7 ep=1e-5;%默认精度 8 else 9 error('输入参数不足');%输入参数必须包括f(x)和[a,b] 10 end 11 if fun(a)*fun(b)>0%输入的区间要求 12 root=[fun(a),fun(b)]; 13 k=0; 14 return; 15 end 16 k=1; 17 while abs(b-a)/2>ep%精度要求 18 mid=(a+b)/2;%中点 19 if fun(a)*fun(mid)<0 20 b=mid; 21 elseif fun(a)*fun(mid)>0 22 a=mid; 23 else 24 a=mid;b=mid; 25 end 26 k=k+1; 27 end 28 root=(a+b)/2; 29 end
运行示例(并未对输出格式做控制,由于精度要求,事后有必要控制输出的精度):

优化代码,减小迭代次数(在迭代前,先搜寻更适合的有根区间)

1 %二分法改良 2 %在一开始给定的区间中寻找更小的有根区间 3 %输入:f(x)=0的f(x),[a,b]的a,b,精度ep 4 %输出:近似根root,迭代次数k 5 %得到的根是优化区间里的最大根 6 function [root,k]=bisect3(fun,a,b,ep) 7 if nargin>3 8 elseif nargin<4 9 ep=1e-5;%默认精度 10 else 11 error('输入参数不足');%输入参数必须包括f(x)和[a,b] 12 end 13 %定义划分区间的分数 14 divQJ=1000; 15 %等分区间 16 tX=linspace(a,b,divQJ); 17 %计算函数值 18 tY=fun(tX); 19 %找到函数值的正负变化的位置 20 locM=find(tY<0); 21 locP=find(tY>0); 22 %定义新区间 23 if tY(1)<0 24 a=tX(locM(end)); 25 b=tX(locP(1)); 26 else 27 a=tX(locP(end)); 28 b=tX(locM(1)); 29 end 30 if fun(a)*fun(b)>0%输入的区间要求 31 root=[fun(a),fun(b)]; 32 k=0; 33 return; 34 end 35 k=1; 36 while abs(b-a)/2>ep%精度要求 37 mid=(a+b)/2;%中点 38 if fun(a)*fun(mid)<0 39 b=mid; 40 elseif fun(a)*fun(mid)>0 41 a=mid; 42 else 43 a=mid;b=mid; 44 end 45 k=k+1; 46 end 47 root=(a+b)/2; 48 end
运行示例(同样没有控制输出)

明显地,迭代次数减小许多。
继续优化代码,以获得区间里所有的根(关键是对有根区间的判断与记忆)

1 %二分法改良 2 %在一开始给定的区间中寻找更小的有根区间 3 %输入:f(x)=0的f(x),[a,b]的a,b,精度ep 4 %输出:近似根root,迭代次数k 5 %例子: 6 %fun=inline('x.^3-x.^2-4*x+4');a=-3;b=3;ep=1e-5; 7 %fun=inline('x.^2-1');a=-2;b=2;ep=1e-5; 8 %fun=inline('-x.^2+1');a=-2;b=2;ep=1e-5; 9 %fun=inline('x.^2-3*x+2');a=0;b=3;ep=1e-5; 10 function [root,k,x,y]=bisect4(fun,a,b,ep) 11 if nargin>3 12 elseif nargin<4 13 ep=1e-5;%默认精度 14 else 15 error('输入参数不足');%输入参数必须包括f(x)和[a,b] 16 end 17 %定义划分区间的分数 18 divQJ=100; 19 %等分区间 20 tX=linspace(a,b,divQJ); 21 %计算函数值 22 tY=fun(tX); 23 %找到函数值的正负变化的位置 24 locM=find(tY<0); 25 locP=find(tY>0); 26 %得到的符号序列,找其中的间断点 27 z=0; 28 k=1; 29 for i=1:length(locM)-1%扫描-符号序列 30 %滚筒算法 31 if(i==1 && locM(1)~=1) 32 z=z+1; 33 x(z)=locM(i); 34 end 35 tmp=locM(i+1)-locM(i); 36 if(tmp~=1) 37 z=z+1; 38 x(z)=locM(i); 39 z=z+1; 40 x(z)=locM(i+1); 41 end 42 end 43 44 l=0; 45 for i=1:length(locP)-1%扫描+符号序列 46 %滚筒算法 47 if(i==1 && locP(1)~=1) 48 l=l+1; 49 y(l)=locP(i); 50 end 51 tmp=locP(i+1)-locP(i); 52 if(tmp~=1) 53 l=l+1; 54 y(l)=locP(i); 55 l=l+1; 56 y(l)=locP(i+1); 57 end 58 end 59 if(z==l-1) 60 z=z+1; 61 x(z)=locM(end); 62 elseif(z==l+1) 63 l=l+1; 64 y(l)=locP(i); 65 end 66 67 if(z==0 && l==0) 68 if(locM(end)<locP(1)) 69 x(1)=locM(end); 70 y(1)=locP(1); 71 else 72 x(1)=locM(1); 73 y(1)=locP(end); 74 end 75 z=1; 76 elseif(z==0) 77 x(1)=locM(1); 78 x(2)=locM(end); 79 z=2; 80 elseif(l==0) 81 y(1)=locP(1); 82 y(2)=locP(end); 83 z=2; 84 end 85 for i=1:z 86 a=tX(x(i)); 87 b=tX(y(i)); 88 if fun(a)*fun(b)>0%输入的区间要求 89 root=[fun(a),fun(b)]; 90 k=0; 91 return; 92 end 93 if(a>b) 94 tmp=b; 95 b=a; 96 a=tmp; 97 end 98 while abs(b-a)/2>ep%精度要求 99 mid=(a+b)/2;%中点 100 if fun(a)*fun(mid)<0 101 b=mid; 102 elseif fun(a)*fun(mid)>0 103 a=mid; 104 else 105 a=mid;b=mid; 106 end 107 k=k+1; 108 end 109 root(i)=(a+b)/2; 110 end 111 end
运行示例(仍然没有控制输出,笔者忽然觉得自己中了月亮的毒!!!)




使用二分法解得在[0,1]上的 根为0.090526。(终于在最后回答问题时做了<_> 控制输出的方法:在调用函数前,在控制台输入format long;得到一long型的数据,根据精度读取。)
根为0.090526。(终于在最后回答问题时做了<_> 控制输出的方法:在调用函数前,在控制台输入format long;得到一long型的数据,根据精度读取。)
(2)不动点迭代算法与MATLAB程序。



1 %不动点迭代法 2 %输入:fun函数,初始值x0,精度ep,最大迭代次数Nmax 3 %输出:近似根root,迭代次数k 4 function [root, k]=iterate(fun,x0,ep,Nmax) 5 if nargin<4 6 Nmax=500; 7 end 8 if nargin<3 9 ep=1e-5; 10 end 11 x=x0; 12 x0=x+2*ep; 13 k=0; 14 while abs(x0-x)>ep && k<Nmax 15 x0=x; 16 x=fun(x0); 17 k=k+1; 18 end 19 root=x; 20 if k==Nmax 21 warning('已达到迭代次数上限'); 22 end 23 end
运行示例(对迭代方程的简单推导得到: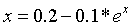 ):
):

就没优化的二分法与不动点迭代法比较,明显地迭代法的迭代次数更少。
使用不动点迭代法,求得近似根0.090525。
小结
就上述两个程序而言,二分法的编程更具挑战。在优化二分法的程序过程中,发现二分法的关键就在于对所给定区间的讨论划分。得到一个能求解给定区间里的所有零点的程序的关键是(分类讨论的思想),对符号变化的记录与使用,换言之,解决这个问题的关键就在于分支结构的使用。
(不可否认,第三个二分法程序仍然有bug!!!待解决——有空再说。)
