实验目的
(1) 直观了解回归分析基本内容;
(2)掌握用数学软件求解回归分析问题。
实验要求
实验步骤要有模型建立,模型求解、结果分析。
实验内容
(1)考察温度x对产量y的影响,测得下列10组数据:

求y关于x的线性回归方程,检验回归效果是否显著,并预测x=42℃时产量的估值及预测区间(置信度95%).
(2)某零件上有一段曲线,为了在程序控制机床上加工这一零件,需要求这段曲线的解析表达式,在曲线横坐标xi处测得纵坐标yi共11对数据如下:

求这段曲线的纵坐标y关于横坐标x的二次多项式回归方程.
(3)混凝土的抗压强度随养护时间的延长而增加,现将一批混凝土作成12个试块,记录了养护日期x(日)及抗压强度y(kg/cm2)的数据:

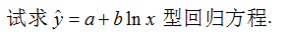
实验步骤

使用MATLAB求解问题(1),代码

1 %回归分析 2 x=20:5:65; 3 Y=[13.2,15.1,16.4,17.1,17.9,18.7,... 4 19.6,21.2,22.5,24.3]; 5 X=[ones(length(x),1),x']; 6 [b,bint,r,rint,stats]=regress(Y',X) 7 sigga2=sum(r.^2)/(length(x)-2); 8 %Sx2=var(x); 9 Lxx=var(x)*(length(x)-1); 10 z=b(1)+b(2)*x; 11 figure(1),hold on; 12 plot(x,Y,'k+',x,z,'r','LineWidth',2,'LineWidth',2); 13 legend('原始数据','回归方程','Location','southeast'); 14 grid on; 15 figure(2),rcoplot(r,rint); 16 %set(gca,'Color','w');

于是算得预测值的置信区间为(17.9243, 19.0527),求解的MATLAB命令如下:
>> exp61
>> y=b(1)+b(2)*42;
>> x_bar=mean(x);
>> u=sigga2*2.306*sqrt(1+0.1+(42-x_bar)^2/Lxx);
>> a=y-u;
>> b=y+u;
代码输出的图:
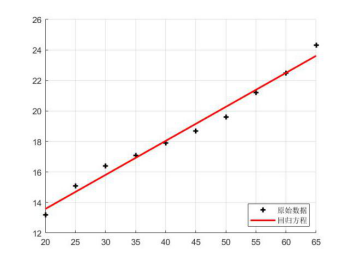

图1 回归方程拟合图和残差图
使用SPSS求解系数,
|
系数a |
||||||||
|
模型 |
未标准化系数 |
标准化系数 |
t |
显著性 |
B 的 95.0% 置信区间 |
|||
|
B |
标准错误 |
Beta |
下限 |
上限 |
||||
|
1 |
(常量) |
9.121 |
.477 |
19.119 |
.000 |
8.021 |
10.221 |
|
|
温度 |
.223 |
.011 |
.991 |
20.972 |
.000 |
.199 |
.248 |
|
|
a. 因变量:产量 |
||||||||
同样算得y=9.121+0.223x,并且显著性为0.000<0.05,回归方程具有意义。
代码:

1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS CI(95) R ANOVA CHANGE 4 /CRITERIA=PIN(.05) POUT(.10) 5 /NOORIGIN 6 /DEPENDENT 产量 7 /METHOD=ENTER 温度 8 /RESIDUALS DURBIN 9 /SAVE PRED.
(2)解:设y=ax2+bx+c,使用MATLAB求解
>> x=0:2:20;y=[0.6,2.0,4.4,7.5,11.8,17.1,23.3,31.2,39.6,49.7,61.7];
>> [p,s]=polyfit(x,y,2);yy=@(x)p(1).*x.^2+p(2).*x+p(3);
>> x=linspace(0,20,40);hold on;
>> title('0.1403*x^2+0.1971*x+1.0105'),
>> plot(0:2:20,y,'ko',x,yy(x),'b','LineWidth',3);
>> legend('原始数据','回归方程');grid on;
算得a=0.1403,b=0.1971,c=1.0105。回归方程:y=0.1403x2+0.1971x+1.0105
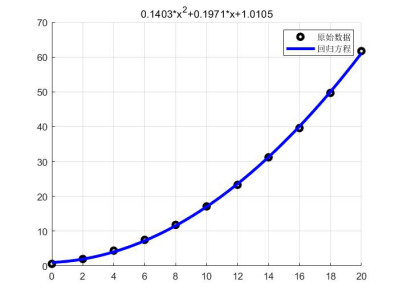
图2 题2的回归方程拟合图
(3)解:由题干给出的y=a+blnx,并使用MATLAB求解,首先给出volum61.m文件

1 function yhat=volum61(beta,x) 2 yhat=beta(1)+beta(2).*log(x); 3 end
命令行求解:
>> x=[2,3,4,5,7,9,12,14,17,21,28,56];
>> y=[35,42,47,53,59,65,73,76,82,86,99];
>> x=[2,3,4,5,7,9,12,14,17,21,28,56];
>> y=[35,42,47,53,59,65,68,73,76,82,86,99];
>> beta0=[5,1]';
>> [beta,r,J]=nlinfit(x',y','volum61',beta0);
>> beta
beta =
21.0058
19.5285
作图,
>> figure,hold on;
>> xx=linspace(2,56,100);
>> yy=volum61(beta,xx);
>> plot(x,y,'o',xx,yy,'Linewidth',2,'Linewidth',2);
>> title('y=21.0058+19.5285lnx');
>> legend('原始数据','回归方程','Location','southeast');grid on;
图3 题3的回归方程拟合图
由图可见回归方程的效果很好。
小结
在求解回归分析的题目时,其中印象最深刻的应该是题1的求解,它用到了概率论与数理统计的知识。然后后面的两题,似乎用到了拟合的知识。
