第4章 数值积分与数值微分
1、见下图:

2、如果某个求积公式对次数不超过m的多项式均能准确成立,但对于m+1次多项式就不能准确成立,则称该求积公式具有m次代数精度。梯形公式和中矩形公式的代数精度为1.
3、由于是给定求积公式的节点,因此,不能使用高斯型求积公式;由于未说明是等距节点,因此不能用牛顿-科特斯求积公式。可使用插值型求积公式和机械求积。
4、见下图:

5、见下图:

6、见下图:

7、见下图:

8、龙贝格求积公式也称为逐次分半加速法,它是在梯形公式、辛普森公式和科特斯公式之间的关系的基础上,构造出一种加速计算积分的方法。使用理查森外推算法,它在不增加计算量的前提下提高了误差的精度。在等距基点的情况下,用计算机积分值通常都采用把区间逐次分半的方法进行。这样,前一次分割得到的函数值在分半以后仍可被利用,且易于编程。龙贝格算法公式,见下图;
![]()
9、见下图:

10、牛顿-科特斯求积节点等距分布,高斯求积的节点分布是插值型多项式的零件。对同样数目的节点,高斯求积更精确。
11、如果求积区间中被积函数变化很大,有部分函数值变化剧烈,需要使用小步长,另一部分函数值变化平缓,可以使用大步长,针对被积函数在区间上的不同情形采用不同的步长,使得在满足精度前提下积分计算工作量尽可能小,针对这类问题的算法技巧是在不同区间上预测被积函数变化的剧烈程度确定响应步长。就是自动求积的一般步骤。
12、见下图:
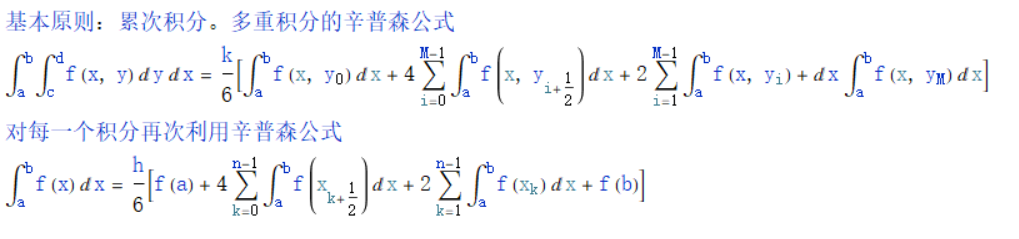
13、。
14、(1)✔;
(2)✖;
(3)✖,是衡量计算准确度的一个指标。
(4)✔;
(5)✖,可以通过变化使得计算时区在[-1,1]上。
(6)✖,典型例子是,当n为偶数时,牛顿-科特斯公式至少为n+1阶代数精度。
(7)✖,梯形公式,代数精度为1,两点高斯公式代数精度为3.
(8)✔;
(9)✖,龙贝格精度为2n,牛顿-科特斯进度最大为n+1;
(10)✖。