1.基础的六种常用排序
冒泡排序
选择排序
插入排序
希尔排序
归并排序
快速排序
2.六种常用排序通用工具类
package com.meijs.algorithm.util;
public class SortUtil {
// 比较v元素是否大于w元素
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
// 数组元素i和j交换位置
public static void exch(Comparable[] a,int i,int j){
Comparable t = a[i];
a[i]=a[j];
a[j]=t;
}
}
3.冒泡排序原理,代码及算法复杂度分析
排序前:{4,5,6,3,2,1}
排序后:{1,2,3,4,5,6}
排序原理:
比较相邻的元素。如果前一个元素比后一个元素大,就交换这两个元素的位置。
对每一对相邻元素做同样的工作,从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大值。

代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 冒泡排序
*/
public class BubbleSort {
public static void main(String args[]){
Integer[] a = {4, 5, 6, 3, 2, 1};
sort(a);
System.out.println(Arrays.toString(a));
}
private static void sort(Comparable[] a){
for(int i=a.length-1;i>0;i--){
for (int j = 0; j <i; j++) {
if (SortUtil.greater(a[j],a[j+1])){
SortUtil.exch(a,j,j+1);
}
}
}
}
}
复杂度分析
冒泡排序使用了双层for循环,其中内层循环的循环体是真正完成排序的代码,所以分析冒泡排序的时间复杂度,主要分析一下内层循环体的执行次数即可。
在最坏情况下,也就是假如要排序的元素为{6,5,4,3,2,1}逆序,那么:
元素比较的次数为:(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2
元素交换的次数为:(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2
总执行次数为:(N^2/2-N/2)+(N^2/2-N/2)=N^2-N
按照大O推导法则,保留函数中的最高阶项那么最终冒泡排序的时间复杂度为O(N^2)
4.选择排序原理,代码及算法复杂度分析
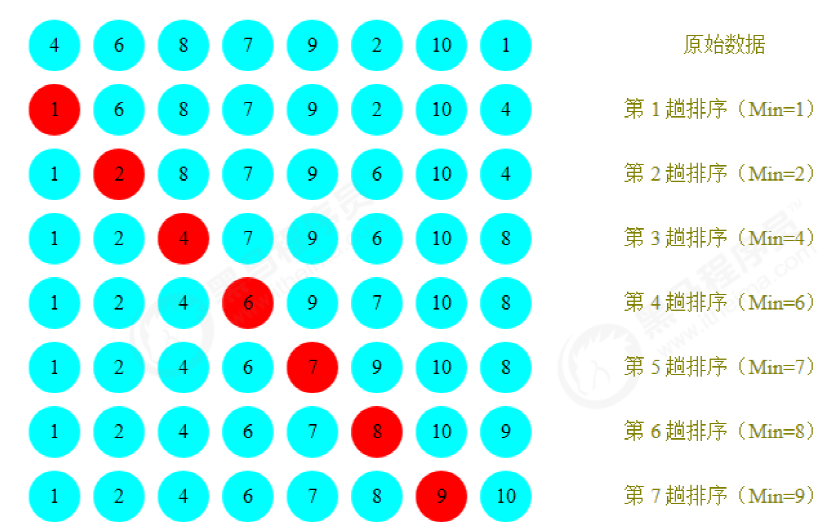
排序前:{4,6,8,7,9,2,10,1}
排序后:{1,2,4,5,7,8,9,10}
排序原理:
每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引
交换第一个索引处和最小值所在的索引处的值
代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 选择排序
*/
public class SelectionSort {
public static void main(String args[]) {
Integer[] a = {4, 6, 8, 7, 9, 2, 10, 1};
SelectionSort.sort(a);
System.out.println(Arrays.toString(a));
}
public static void sort(Comparable[] a) {
for (int i = 0; i <= a.length - 2; i++) {
//假定本次遍历,最小值所在的索引是i
int minIndex = i;
for (int j = i + 1; j < a.length; j++) {
if (SortUtil.greater(a[minIndex], a[j])) {
//跟换最小值所在的索引
minIndex = j;
}
}
//交换i索引处和minIndex索引处的值
SortUtil.exch(a, i, minIndex);
}
}
}
复杂度分析
选择排序使用了双层for循环,其中外层循环完成了数据交换,内层循环完成了数据比较,所以我们分别统计数据交换次数和数据比较次数:
数据比较次数:(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2
数据交换次数:N-1
时间复杂度:N^2/2-N/2+(N-1)=N^2/2+N/2-1
根据大O推导法则,保留最高阶项,去除常数因子,时间复杂度为O(N^2)
5.插入排序原理,代码及算法复杂度分析
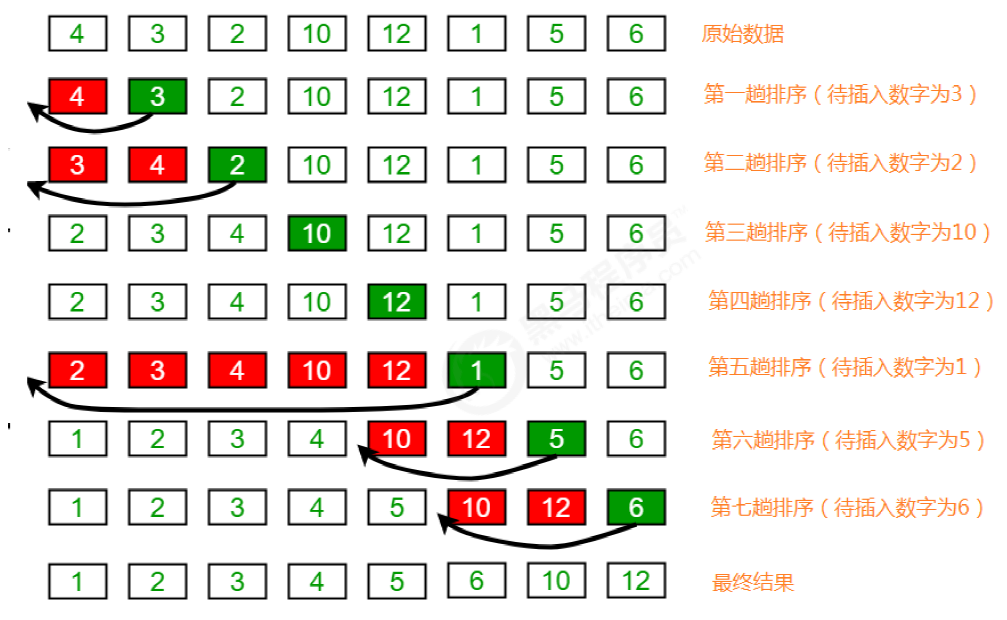
排序前:{4,3,2,10,12,1,5,6}
排序后:{1,2,3,4,5,6,10,12}
排序原理:
把所有的元素分为两组,已经排序的和未排序
找到未排序的组中的第一个元素,向已经排序的组中进行插入
倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于等于待插入元素,那么就把待插入元素放到这个位置,其他的元素向后移动一位;
代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 插入排序
*/
public class InsertionSort {
public static void main(String args[]){
Integer[] a = {4,3,2,10,12,1,5,6};
InsertionSort.sort(a);
System.out.println(Arrays.toString(a));
}
public static void sort(Comparable[] a) {
for (int i = 1; i < a.length; i++) {
//当前元素为a[i],依次和i前面的元素比较,找到一个小于等于a[i]的元素
for (int j = i; j > 0; j--) {
if (SortUtil.greater(a[j - 1], a[j])) {
//交换元素
SortUtil.exch(a, j - 1, j);
} else {
//找到了该元素,结束
break;
}
}
}
}
}
复杂度分析
插入排序使用了双层for循环,其中内层循环的循环体是真正完成排序的代码,所以,我们分析插入排序的时间复杂度,主要分析一下内层循环体的执行次数即可。
最坏情况,也就是待排序的数组元素为{12,10,6,5,4,3,2,1},那么:
比较的次数为:(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2
交换的次数为:(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2
总执行次数为:(N^2/2-N/2)+(N^2/2-N/2)=N^2-N
按照大O推导法则,保留函数中的最高阶项那么最终插入排序的时间复杂度为O(N^2)
6.希尔排序原理,代码及算法复杂度分析
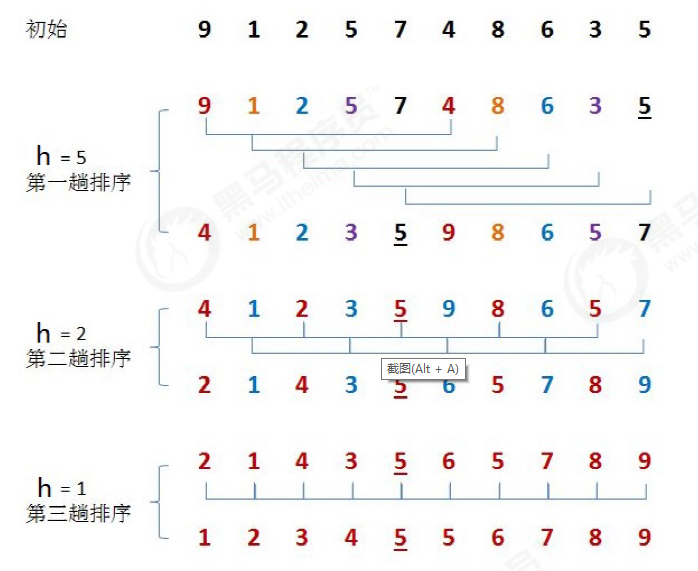
排序前:{9,1,2,5,7,4,8,6,3,5}
排序后:{1,2,3,4,5,5,6,7,8,9}
排序原理:
选定一个增长量h,按照增长量h作为数据分组的依据,对数据进行分组
对分好组的每一组数据完成插入排序
减小增长量,最小减为1,重复第二步操作。
代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 希尔排序
*/
public class ShellSort {
public static void main(String args[]){
Integer[] a = {9,1,2,5,7,4,8,6,3,5};
ShellSort.sort(a);
System.out.println(Arrays.toString(a));
}
public static void sort(Comparable[] a){
int N = a.length;
//确定增长量h的最大值
int h=1;
while(h<N/2){
h=h*2+1;
}
//当增长量h小于1,排序结束
while(h>=1){
//找到待插入的元素
for (int i=h;i<N;i++){
//a[i]就是待插入的元素
//把a[i]插入到a[i-h],a[i-2h],a[i-3h]...序列中
for (int j=i;j>=h;j-=h){
//a[j]就是待插入元素,依次和a[j-h],a[j-2h],a[j-3h]进行比较,如果a[j]小,那么交换位置,如果不小于,a[j]大,则插入完成。
if (SortUtil.greater(a[j-h],a[j])){
SortUtil.exch(a,j,j-h);
}else{
break;
}
}
}
h/=2;
}
}
}
复杂度分析
在希尔排序中,增长量h并没有固定的规则,有很多论文研究了各种不同的递增序列,但都无法证明某个序列是最好的,故希尔排序的时间复杂度分析是一个动态的,较为复杂,这里就不做分析了。但是肯定的是,在数据量巨大的情况下。希尔排序比以上排序都要快很多。在小数据量的排序上,可能看不出直观的差别
7.归并排序原理,代码及算法复杂度分析
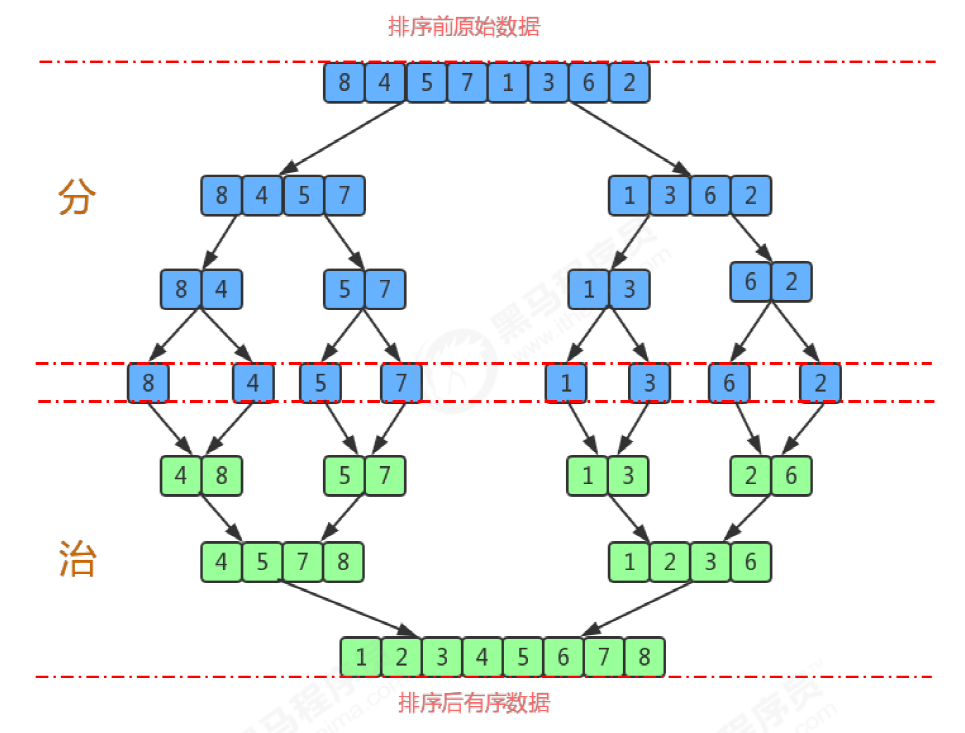
排序前:{8,4,5,7,1,3,6,2}
排序后:{1,2,3,4,5,6,7,8}
排序原理:
尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是为止
将相邻的两个子组进行合并成一个有序的大组
不断的重复第二次,直到最终只有一个组为止
归并排序本质上是一种分而治之的思想,这种思想在大数据中最为常见
代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 归并排序
*/
public class MergeSort {
private static Comparable[] assist;//归并所需要的辅助数组
public static void main(String args[]) {
Integer[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
MergeSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a) {
assist = new Comparable[a.length];
int lo = 0;
int hi = a.length - 1;
sort(a, lo, hi);
}
/*
对数组a中从lo到hi的元素进行排序
*/
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) {
return;
}
int mid = lo + (hi - lo) / 2;
//对lo到mid之间的元素进行排序;
sort(a, lo, mid);
//对mid+1到hi之间的元素进行排序;
sort(a, mid + 1, hi);
//对lo到mid这组数据和mid到hi这组数据进行归并
merge(a, lo, mid, hi);
}
/*
对数组中,从lo到mid为一组,从mid+1到hi为一组,对这两组数据进行归并
*/
private static void merge(Comparable[] a, int lo, int mid, int hi) {
//lo到mid这组数据和mid+1到hi这组数据归并到辅助数组assist对应的索引处
int i = lo;//定义一个指针,指向assist数组中开始填充数据的索引
int p1 = lo;//定义一个指针,指向第一组数据的第一个元素
int p2 = mid + 1;//定义一个指针,指向第二组数据的第一个元素
//比较左边小组和右边小组中的元素大小,哪个小,就把哪个数据填充到assist数组中
while (p1 <= mid && p2 <= hi) {
if (SortUtil.greater(a[p1], a[p2])) {
assist[i++] = a[p1++];
} else {
assist[i++] = a[p2++];
}
}
//上面的循环结束后,如果退出循环的条件是p1<=mid,则证明左边小组中的数据已经归并完毕,如果退出循环的条件是p2<=hi,则证明右边小组的数据已经填充完毕;
//所以需要把未填充完毕的数据继续填充到assist中,//下面两个循环,只会执行其中的一个
while (p1 <= mid) {
assist[i++] = a[p1++];
}
while (p2 <= hi) {
assist[i++] = a[p2++];
}
//到现在为止,assist数组中,从lo到hi的元素是有序的,再把数据拷贝到a数组中对应的索引处
for (int index = lo; index <= hi; index++) {
a[index] = assist[index];
}
}
}
复杂度分析
归并排序是分治思想的最典型的例子,上面的算法中,对a[lo...hi]进行排序,先将它分为a[lo...mid]和a[mid+1...hi]两部分,分别通过递归调用将他们单独排序,最后将有序的子数组归并为最终的排序结果。该递归的出口在于如果一个数组不能再被分为两个子数组,那么就会执行merge进行归并,在归并的时候判断元素的大小进行排序。
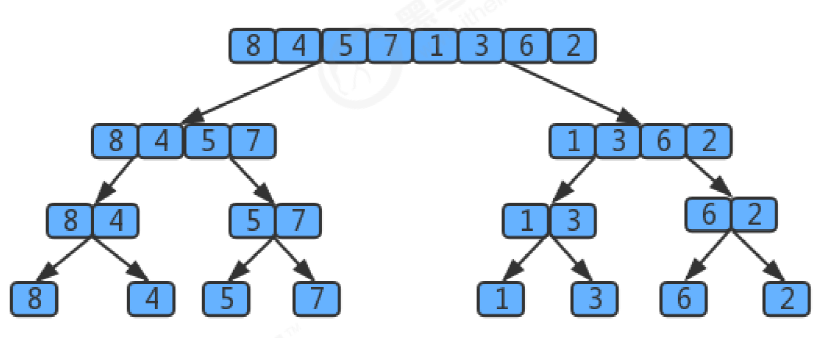
用树状图来描述归并,如果一个数组有8个元素,那么它将每次除以2找最小的子数组,共拆log8次,值为3,所以树共有3层,那么自顶向下第k层有2k个子数组,每个数组的长度为`2^(3-k)`,归并最多需要2(3-k)次比较。因此每层的比较次数为2^k*2^(3-k)=2^3,那么3层总共为3*2^3。假设元素的个数为n,那么使用归并排序拆分的次数为log2(n),所以共log2(n)层,那么使用log2(n)替换上面3*2^3中的3这个层数,最终得出的归并排序的时间复杂度为:log2(n)* 2^(log2(n))=log2(n)*n,根据大O推导法则,忽略底数,最终归并排序的时间复杂度为O(nlogn);
希尔排序和归并排序在处理大批量数据时差别不是很大。
8.快速排序原理,代码及算法复杂度分析
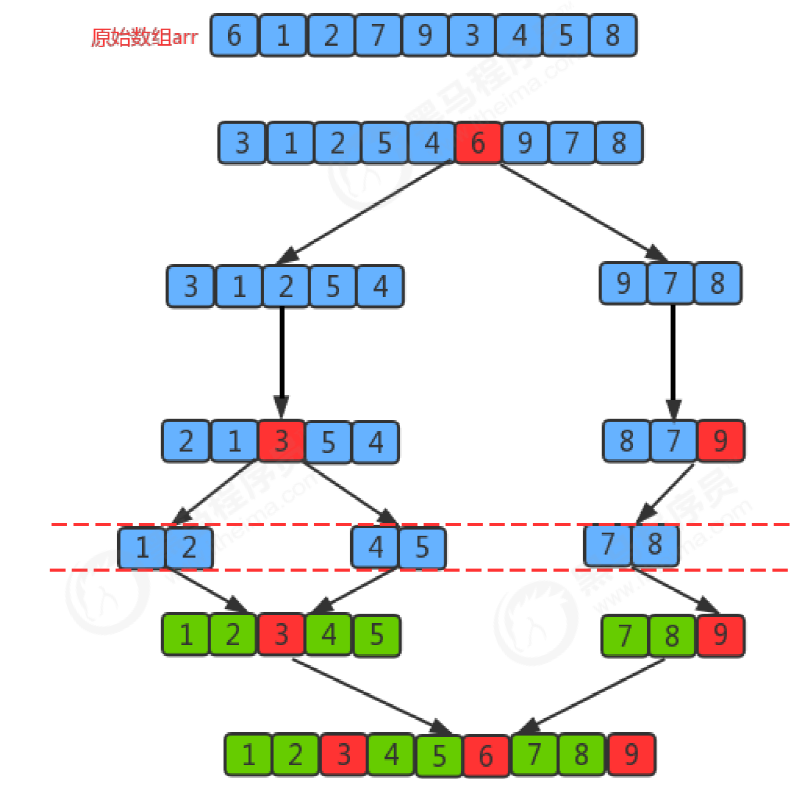
排序前:{6, 1, 2, 7, 9, 3, 4, 5, 8}
排序后:{1, 2, 3, 4, 5, 6, 7, 8, 9}
排序原理:
首先设定一个分界值,通过该分界值将数组分成左右两部分
将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值
然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后,整个数组的排序也就完成了。
代码实现
package com.meijs.algorithm;
import com.meijs.algorithm.util.SortUtil;
import java.util.Arrays;
/**
* 快速排序
*/
public class QuickSort {
public static void main(String args[]){
Integer[] arr = {6, 1, 2, 7, 9, 3, 4, 5, 8};
QuickSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
//对数组内的元素进行排序
public static void sort(Comparable[] a) {
int lo = 0;
int hi = a.length-1;
sort(a,lo,hi);
}
//对数组a中从索引lo到索引hi之间的元素进行排序
private static void sort(Comparable[] a, int lo, int hi) {
//安全性校验
if (hi<=lo){
return;
}
//需要对数组中lo索引到hi索引处的元素进行分组(左子组和右子组);
int partition = partition(a, lo, hi);//返回的是分组的分界值所在的索引,分界值位置变换后的索引
//让左子组有序
sort(a,lo,partition-1);
//让右子组有序
sort(a,partition+1,hi);
}
//对数组a中,从索引 lo到索引 hi之间的元素进行分组,并返回分组界限对应的索引
public static int partition(Comparable[] a, int lo, int hi) {
//确定分界值
Comparable key = a[lo];
//定义两个指针,分别指向待切分元素的最小索引处和最大索引处的下一个位置
int left=lo;
int right=hi+1;
//切分
while(true){
//先从右往左扫描,移动right指针,找到一个比分界值小的元素,停止
while(SortUtil.greater(key, a[--right])){
if (right==lo){
break;
}
}
//再从左往右扫描,移动left指针,找到一个比分界值大的元素,停止
while(SortUtil.greater(a[++left],key)){
if (left==hi){
break;
}
}
//判断 left>=right,如果是,则证明元素扫描完毕,结束循环,如果不是,则交换元素即可
if (left>=right){
break;
}else{
SortUtil.exch(a,left,right);
}
}
//交换分界值
SortUtil.exch(a,lo,right);
return right;
}
}
复杂度分析
快速排序的一次切分从两头开始交替搜索,直到left和right重合,因此,一次切分算法的时间复杂度为O(n),但整个快速排序的时间复杂度和切分的次数相关。
最优情况:每一次切分选择的基准数字刚好将当前序列等分。
如果我们把数组的切分看做是一个树,那么上图就是它的最优情况的图示,共切分了logn次,所以,最优情况下快速排序的时间复杂度为O(nlogn);
最坏情况:每一次切分选择的基准数字是当前序列中最大数或者最小数,这使得每次切分都会有一个子组,那么总共就得切分n次,所以,最坏情况下,快速排序的时间复杂度为O(n^2)
快速排序和归并排序的区别:
快速排序是另外一种分治的排序算法,它将一个数组分成两个子数组,将两部分独立的排序。快速排序和归并排序是互补的:归并排序将数组分成两个子数组分别排序,并将有序的子数组归并从而将整个数组排序,而快速排序的方式则是当两个数组都有序时,整个数组自然就有序了。在归并排序中,一个数组被等分为两半,归并调用发生在处理整个数组之前,在快速排序中,切分数组的位置取决于数组的内容,递归调用发生在处理整个数组之后。