二叉树的遍历
二叉树的遍历分先序、中序、后序和层次遍历。实现方式分递归和非递归方式。
这里说说层次遍历。
层次遍历是逐层访问二叉树的每个节点。属于广度优先。常常使用队列的方式。
如图有以下一棵二叉树,它构建的队列形式为:
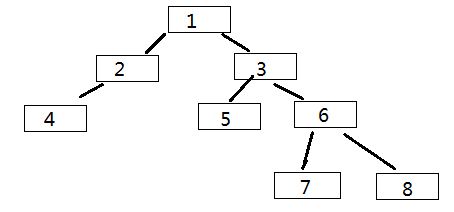
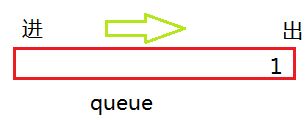
1、先把根节点 1 放入队列,然后弹出,看看它有没有左右孩子,如果有,按顺序将左右孩子放入队列

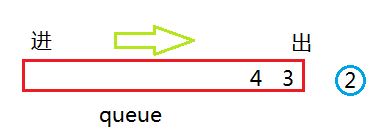
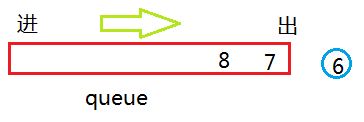
接着按顺序弹出 2 ,看 2 是否还孩子,如果有将2 的孩子加入队列。
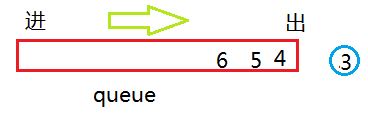
接着弹出 3 看其是否有孩子,如果有依次加入
然后弹出4,看4 是否孩子节点,接着弹出5,看5 是否有孩子节点,如果有 就依次加入队列,显然本例中4 、 5 都没有孩子节点
然后继续弹出6 ,6有孩子节点,依次加入队列,
然后依次弹出7,8这样就对整个二叉树完成了遍历
下面这道题就是根据上图这个方式完成的。
有一棵二叉树,请设计一个算法,按照层次打印这棵二叉树。
给定二叉树的根结点root,请返回打印结果,结果按照每一层一个数组进行储存,所有数组的顺序按照层数从上往下,且每一层的数组内元素按照从左往右排列
本题的关键是 指定两个变量 last 和 nlast 来对节点进行跟踪。
# class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class TreePrinter: def printTree(self, root): # write code here if root == None: return [] queue = [] #定义一个队列,盛放节点 result = [] #定义一个列表,盛放最终结果 temp = [] #定义一个列表,盛放改行所有节点的值。 last = nlast = root #关键:定义两个变量 last nlast 其中:last 永远指向本行最右节点。
#nlast 永远指向 下一行的最右节点 queue.append(root) #首先将root节点 加入队列 while queue: node = queue.pop(0) #弹出队列的第一个节点 temp.append(node.val) #将弹出节点的值,放入temp 列表。 if node.left: queue.append(node.left) #如果弹出节点有左子树,那么将左孩子节点加入队列 nlast = node.left #因为nlast总是执行下一行的最右节点。所以要更新nlast指向。 if node.right: queue.append(node.right) #如果弹出节点有右子树,那么将右孩子加入队列 nlast = node.right # 同时再次更新nlast的指向。 if last == node: #如果弹出节点 == last 指向的节点(last总是指向本行最右节点) 说明一行结束了 last = nlast # 当前行已经结束了,所以更新last使其指向 下一行 的最右节点。 result.append(temp) #将上一行的所有节点的值的结果列表放入最终结果中。 temp = [] # 将temp置空,准备盛放下一行的所有节点的值 return result #返回最终结果