堆排序
在堆排序中,我们可以将顺序表看成一颗完全的二叉树
二叉树知识回顾:
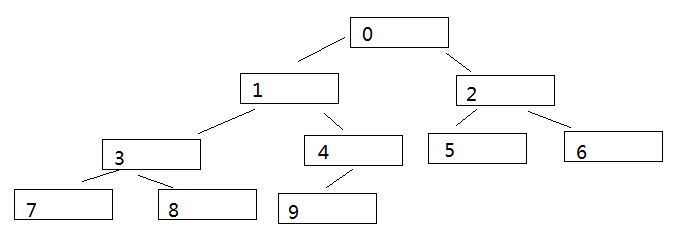
从1开始对二叉树中的每个节点顺序编号
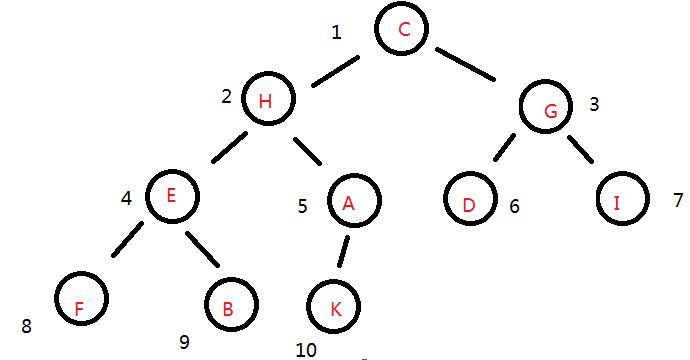
序列 : [ # , C, H, G, E, A, D, I, F, B, K ]
索引 1 2 3 4 5 6 7 8 9 10
所以编号为 i 的 左孩子节点编号为 2*i ; 右孩子节点编号为 2*i+ 1,
除了根节点,如果一个节点编号为 j 那么它的双亲节点为 j//2
如果将序列R[1,n] 视作一个完全二叉树,那么 R[i] 的左孩子是R[2i] 右孩子则为R[2i+1]

堆:
n个值的序列K[1],K[2],K[3]……K[n] 称之为堆。
该序列满足一下特性
大根堆: K[i] >= K[2*i] 且 K[i] > = K[2*i +1] i 的范围 1 ~ n//2
小根堆: K[i] <= K[2*i] 且 K[i] <= K[2*i +1]
如图所示

小根堆

大根堆
堆排序的简单过程是:
1、根据序列,构建一个初始堆 (大根堆/小根堆)
2、交换堆的第一个和最后一个元素。
3、排除最后一个元素,将序列第一个到倒数第二个重新整理成 堆。
4、再次交换堆的第一个和最后一个元素
5、重复 第3 步
6 、重复上述过程直至完成排序
再说简单点就是:构造堆,交换元素、构造堆,交换元素,构造堆。。。。。。
从上述 6步的第三步——交换第一个和最后一个元素,而且该动作会在每次整理完堆之后,都会重复进行。所以我们就知道,序列的最后一个元素总是当前堆的最大/最小元素。所以,第一步,我们究竟是要构建大根堆还是小根堆,是要看我们打算顺序排序序列还是要倒序排序序列。
在下面的例子中我们 顺序排序 序列,也就说 构建 大根堆。
有这样一个序列
A = [ --, 1, 0, 3, 6, 2, 8, 4, 9, 7, 5 ]
构建二叉树,树节点从 1 开始 编号。所以A[0] 为占位作用。初始二叉树如下:

开始构建大根堆。
1、从最后一个非叶子节点开始。比较 节点 和它的 最大 孩子节点,如果 如果节点大,那么就保持不变。如果孩子节点大,那么就交换孩子节点和该节点的值。
在本例中,最后一个非叶子节点是 序号为 5,值为 2 的节点。比较它和它的最大孩子节点。发现5 >2 所以交换他和他的孩子。
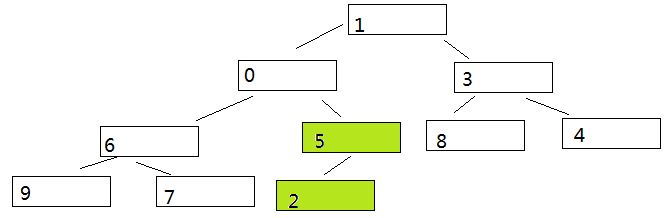
2、然后查看倒数第二个非叶子节点,也就是 序号为4 值为 6 的节点。同样比较它和它的最大孩子节点。发现,6<9 也需要交换[下图中红色部分]
3、然后继续查看倒数第三个非叶子节点,也就是 序号为 3 值为3 的节点,同样比较它和它的最大孩子节点,发现 8>3 ,也需要交换[下图中灰色部分]

4,然后继续比较倒数第四个非叶子节点。即 序号为2 值为 0 的 节点。比较它和它的最大孩子节点 ,发现0<9,交换2者????? 莫急,你再往下看会发现即使0 和 9 交换了,0还是比它现在的最大孩子节点(7)小,所以,还要继续交换 0 和7 最终结果就是下图:

5,接下来移动序号为1,值为1 的节点。。。重复上述过程,最终构造出的大根堆如下:
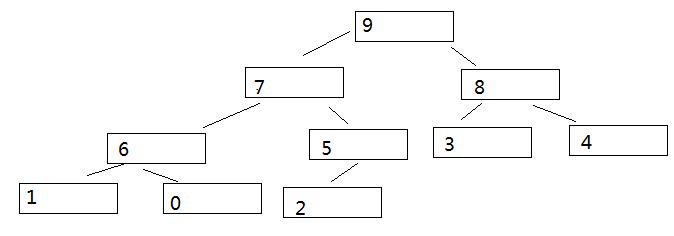
这就是完成构造初始堆的过程。函数如下:

def fixDown(a, i, n): # i 是指当前节点 n 为序列中所有元素的最大索引。二叉树中 最后一个节点的 序号 while 2 * i <= n: # j = 2*i 即 当前节点的左孩子。它必须在所有节点的序号范围内。如果j > n 了说明 i 是叶子节点。 j = 2 * i if j < n and a[j] < a[j + 1]: # 选出左右孩子节点中更大的那个。注意一:下面详说。 j += 1 if a[i] < a[j]: # 如果双亲节点小于孩子节点,那么交换双亲节点和子节点。同时向下移动 i 的位置。i 的范围是[1-n//2] a[i], a[j] = a[j], a[i] i = j else: #如果双亲节点大于他的最大的孩子,那么说明这个小的二叉树构建堆完成。 break
注意一: 这条语句中使用了短路原则。即:如果 j < n 为假那么就不再对后面的条件进行判断。直接跳过该条件语句,进行下面的语句。为什么在本条件语句中 要求 j != n,在本例中 j = 10,如果 条件语句改成 j<= n ,10 <=10,第一个条件成立了,那么无疑会继续验证第二个条件是否成立,然而对照本例你会发现,根本没有第11个节点,即a[j+1] 是不存在的。所以这会给程序引发一个超出索引的错误。
初始化堆的,同时也是整理堆的函数有了,那么接下来就是在堆排序的主函数中调用这个函数,进行堆排序了,还是先用图演示一下,再给代码。
回顾一下上述的 堆排序的过程 。构造堆已经完成了,那么就该交换第一个节点和最后一个节点了。然后,将最后一个节点排除,用剩下的节点再次构建堆。

重新构造堆如下:
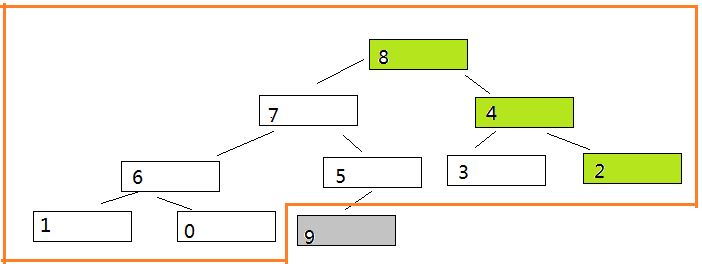
交换第一个和最后一个如下:

重复上面的过程直至再也没有可以构建堆的节点了。排序完成。
代码如下:

def heapSort(A): n = len(A) - 1 # 因为加入了一个占位元素,所以构建堆的实际元素个数应该 减去 1 for i in range(n // 2, 0, -1): #构建初始堆。 从最后一个非叶子节点开始构建堆。地板除 1是为了防止出现小数,2是取下界。 fixDown(A, i,n) # 调用上面的那个构造堆的函数,构造出初始化堆。 print('A=',A) #这里可以看一下 初始化堆之后的序列的 各个元素的排列顺序 while n > 1: # n 表示 堆的最后一个节点的序号 A[1], A[n] = A[n], A[1] # 交换堆的第一个和最后一个 节点 fixDown(A, 1, n-1) # 重新整理堆剩下的节点,再次构建 根堆 n -= 1 # 每次交换之后,已经排好序的节点就被排除出堆,所以堆的最后一个节点的向前移动一位。 return A[1:] #因为我们使用了占位元素,所以返回从 所以为 1 及其以后得元素。 A = [ '--', 1, 0, 3, 6, 2, 8, 4, 9, 7, 5 ] # 第一个元素不用,占位 print(heapSort(A))
这里再说一下:
因为我们是从小到大排列 序列。所以每次都是让 让 A[i] 和他子节点中比较大的那个进行比较,然后大的上浮,小的下沉。从而构建大根堆
如果我们想要从大到小 逆序排列的话
那么就要让 A[i] 和它 的子节点中 较小的那个比较,小的上浮,大的下沉。
所以 构造堆的代码如下:

def fixDown(a, i, n): # i 是指当前节点 n 为序列中所有元素的最大索引。二叉树中 最后一个节点的 序号 while 2 * i <= n: # j = 2*i 即 当前节点的左孩子。它必须在所有节点的序号范围内。如果j > n 了说明 i 是叶子节点。 j = 2 * i if j < n and a[j] > a[j + 1]: # 选出左右孩子节点中更 !!小!! 的那个 j += 1 if a[i] > a[j]: # 如果双亲节点!! 大于 !!孩子节点,那么交换双亲节点和子节点。同时向下移动 i 的位置。i 的范围是[1-n//2] a[i], a[j] = a[j], a[i] i = j else: #如果双亲节点!!小于!!他的!!最小!!的孩子,那么说明这个小的二叉树构建堆完成。 break
