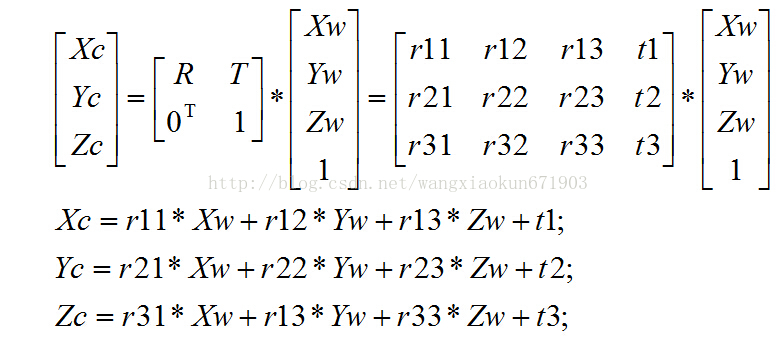一、背景分析:
充分理解不同坐标系,以及它们之间的转换关系对于研究3D几何视图以及VSLAM是非常有必要的。
二、各坐标系间相互关系:
1、世界坐标系到相机坐标系
转换关系主要是外参:R,T
R、T与摄像机无关,所以称这两个参数为摄像机的外参数(extrinsic parameter),可以理解为两个坐标原点之间的距离,因其受x,y,z三个方向上的分量共同控制,所以其具有三个自由度。
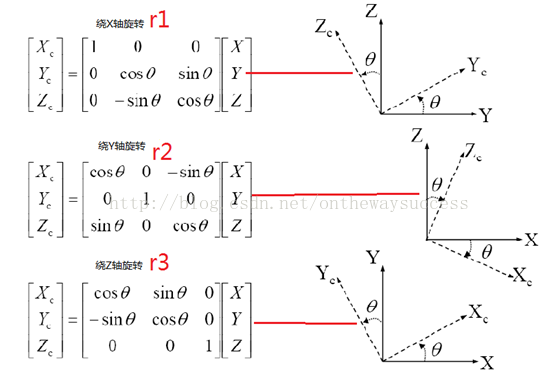
R则为分别绕XYZ三轴旋转的效果之和。如下面所示:
R=r1*r2*r3.其由三个方向的θ控制,故具有三个自由度。
[Xc,Yc,Zc]T表示相机坐标,[Xw,Yw,Zw,1]T表示归物体所在的世界坐标。R表示旋转矩阵,T表示平移矩阵。
2、相机坐标系到图像坐标系
转换关系是内参:f
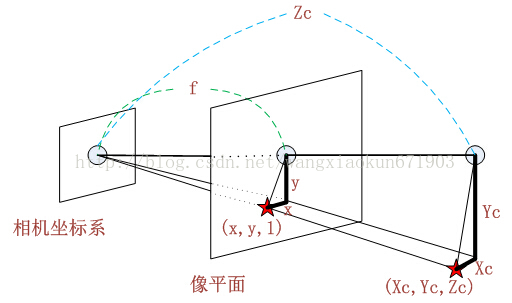
从相机坐标系到图像坐标系,属于透视投影,也即是从3D转换到2D。此时投影点p的单位还是mm,并不是pixel,需要进一步转换到像素坐标系
f表示焦距,[Xc,Yc,Zc]T表示相机坐标。[x,y,1]T表示归一化后的图像物理坐标
3、图像坐标系到像素坐标系
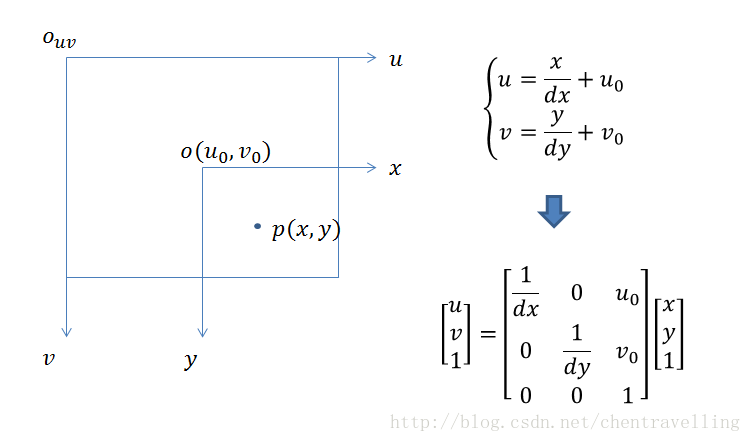
像素坐标系和图像坐标系都在成像平面上,只是各自的原点和度量单位不一样。图像坐标系的原点通常情况下是成像平面的中点,单位是mm,属于物理单位。而像素坐标系的单位是pixel,我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下:其中dx和dy表示每一列和每一行分别代表多少mm,即1pixel=dx mm
三、总转换关系
所以,最后从世界坐标系到像素坐标系的转换公式为: