CART(Classification and Regression tree)分类回归树由L.Breiman,J.Friedman,R.Olshen和C.Stone于1984年提出。CART是一棵二叉树,采用二元切分法,每次把数据切成两份,分别进入左子树、右子树。而且每个非叶子节点都有两个孩子,所以CART的叶子节点比非叶子多。相比ID3和C4.5,CART应用要多一些,既可以用于分类也可以用于回归。
一 特征选择
CART分类时,使用基尼指数(Gini)来选择最好的数据分割的特征,Gini描述的是纯度,与信息熵的含义相似。CART中每一次迭代都会降低GINI系数。下图显示信息熵增益的一半,Gini指数,分类误差率三种评价指标非常接近。回归时使用均方差作为loss function。基尼系数的计算与信息熵增益的方式非常类似,具体的,在分类问题中,假设有K个类别,第k个类别的概率为$p_k$, 则基尼系数的表达式为:
如果是二类分类问题,计算就更加简单了,如果属于第一个样本输出的概率是$p$,则基尼系数的表达式为:
$$Gini(p) = sumlimits_{k=1}^{K}p_k(1-p_k) = 1- sumlimits_{k=1}^{K}p_k^2$$
对于二分类问题来说,基尼系数:
$$Gini(p)=p(1-p)$$
对于个给定的样本D,假设有K个类别, 第k个类别的数量为,则样本D的基尼系数表达式为:
$$Gini(D)=1-sumlimits_{k=1}^{K}(frac{|C_{k}}{|D|}^2$$
特征A条件下的,集合D的基尼系数为:
$$Gini(D,A)=frac{|D_1|}{|D|}Gini(D_1)+ frac{|D_2|}{|D|}Gini(D_2)$$
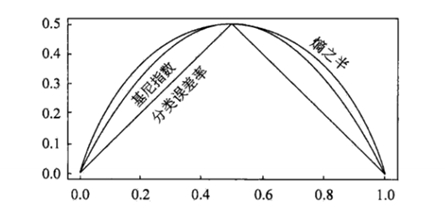
CART中每一次迭代都会降低GINI系数。下图显示信息熵增益的一半,Gini指数,分类误差率三种评价指标非常接近。回归时使用均方差作为loss function。
二 cart用于回归
CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方。
首先,我们要明白,什么是回归树,什么是分类树。两者的区别在于样本输出,如果样本输出是离散值,那么这是一颗分类树。如果果样本输出是连续值,那么那么这是一颗回归树。
除了概念的不同,CART回归树和CART分类树的建立和预测的区别主要有下面两点:
- 连续值的处理方法不同
- 决策树建立后做预测的方式不同。
对于连续值的处理,我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,我们使用了常见的和方差的度量方式,CART回归树的度量目标是,对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为:
$$underbrace{min}_{A,s}Bigg[underbrace{min}_{c_1}sumlimits_{x_i in D_1(A,s)}(y_i - c_1)^2 + underbrace{min}_{c_2}sumlimits_{x_i in D_2(A,s)}(y_i - c_2)^2Bigg]$$
其中,$c_1$为D1数据集的样本输出均值,$c_2$为D2数据集的样本输出均值。
对于决策树建立后做预测的方式,上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。
除了上面提到了以外,CART回归树和CART分类树的建立算法和预测没有什么区别