堆排序(Heap Sort),是指将整个数组转化成“堆”这种数据结构,利用堆的性质,去简化排序的过程。堆排序,可以看做是“变治法”的一种实现。
From Wikipedia:https://en.wikipedia.org/wiki/Heapsort
1. 堆
堆是一种特殊的二叉树结构,但是堆总是需要满足以下两条性质:
- 堆是一棵完全二叉树。即树的每一层都是满的,除了最后一层最右边的元素有可能出现缺位。
- 父母优势。即堆中的所有子节点,总是不大于或不小于其父节点的值。
根据子节点与父节点的关系,可以将堆分为最大堆和最小堆两种情况。
2. 堆的数组表现形式
数组 { 9, 7, 3, 5, 1, 2, 6, 0, 8, 4 } ,可以转化为以下二叉树结构。(目前不具备堆的性质)
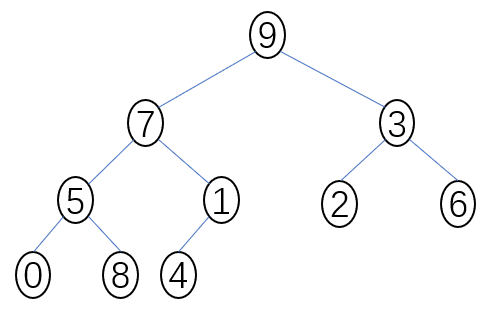
3. 堆的性质(仅罗列在堆排序中用到的性质)
3.1 获取堆中某个节点的左节点、右节点、父节点
public static int left(int i) {
return (i << 1) + 1;
}
public static int right(int i) {
return (i << 1) + 2;
}
public static int parent(int i) {
return (i - 1) >>> 1;
}
3.2 保持最大堆/最小堆的性质
当二叉树中的某个子节点,其左子树和右子树都具备堆的性质,那么可以通过一系列的交换,将以该子节点为根节点的树,转化为堆的结构。
public static void maxHeapify(int[] array, int rootIndex, int lastIndex) {
int l = left(rootIndex);
int r = right(rootIndex);
int largestIndex = rootIndex;
if (l <= lastIndex && array[l] > array[largestIndex]) {
largestIndex = l;
}
if (r <= lastIndex && array[r] > array[largestIndex]) {
largestIndex = r;
}
if (rootIndex != largestIndex) {
ArrayHelper.swap(array, rootIndex, largestIndex);
maxHeapify(array, largestIndex, lastIndex);
}
}
3.3 构造最大堆/最小堆
将一个不具备堆性质的数组,转化为堆的结构,一般都是自底向上开始的。
自二叉树的第一个非叶节点开始,自底向上,依次保持二叉树的堆的性质,直至根节点。
public static void buildMaxHeap(int[] array) {
int lastNonLeaf = (array.length - 2) >>> 1;
for (int i = lastNonLeaf; i > -1; --i) {
maxHeapify(array, i);
}
}
4. 堆排序
在了解了堆的各种性质之后,堆排序就显得非常简单了。
- 第一步:将原数组转化为堆的形式。(升序排列使用最大堆,降序排列使用最小堆,此处假定进行升序排列)
- 第二步:将数组最后一位与第一位交换,因为是最大堆的关系,第一位数字就是最大值,落在了最后一位上。
- 第三步:剔除最后一位数字,将数组剩余部分,看作一颗新的二叉树。其中根节点的左子树和右子树都满足最大堆的性质,保持这棵新二叉树的最大堆性质。
- 第四步:循环第二步,第三步,直至根节点,整个数组即自然有序。
public void sort(int[] array) {
HeapHelper.buildMaxHeap(array);
for (int i = array.length - 1; i > 0; --i) {
ArrayHelper.swap(array, i, 0);
HeapHelper.maxHeapify(array, 0, i - 1);
}
}
5. 堆排序的演练过程
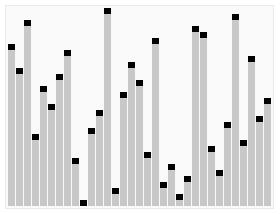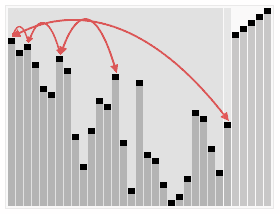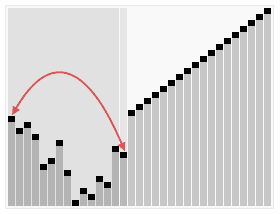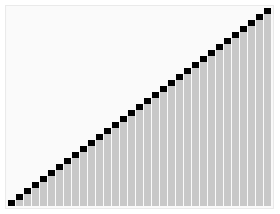
以下演示堆排序在数组 { 9, 7, 3, 5, 1, 2, 6, 0, 8, 4 } 上的应用:
- 构建最大堆:{ 9, 8, 6, 7, 4, 2, 3, 0, 5, 1 }
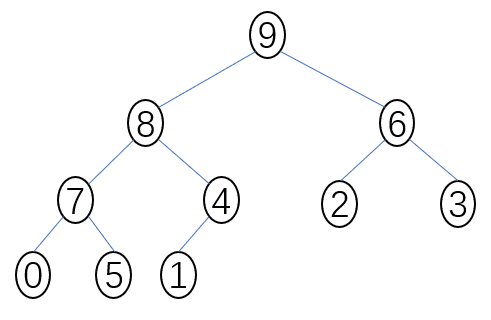
- 交换第一位和最后一位:{ 1, 8, 6, 7, 4, 2, 3, 0, 5, 9 }
- 保持二叉树 { 1, 8, 6, 7, 4, 2, 3, 0, 5 } 的最大堆性质,得到新的数组:{ 8, 7, 6, 5, 4, 2, 3, 0, 1, 9 }
- 交换第一位和倒数第二位:{ 1, 7, 6, 5, 4, 2, 3, 0, 8, 9 }
- 保持二叉树 { 1, 7, 6, 5, 4, 2, 3, 0 } 的最大堆性质,得到新的数组:{ 7, 5, 6, 1, 4, 2, 3, 0, 8, 9 }
- 交换第一位和倒数第三位:{ 0, 5, 6, 1, 4, 2, 3, 7, 8, 9 }
- 保持二叉树 { 0, 5, 6, 1, 4, 2, 3 } 的最大堆性质,得到新的数组: { 6, 5, 3, 1, 4, 2, 0, 7, 8, 9 }
- 交换第一位和倒数第四位:{ 0, 5, 3, 1, 4, 2, 6, 7, 8, 9 }
- 保持二叉树 { 0, 5, 3, 1, 4, 2 } 的最大堆性质,得到新的数组: { 5, 4, 3, 1, 0, 2, 6, 7, 8, 9 }
- 交换第一位和倒数第五位:{ 2, 4, 3, 1, 0, 5, 6, 7, 8, 9 }
- 保持二叉树 { 2, 4, 3, 1, 0 } 的最大堆性质,得到新的数组:{ 4, 2, 3, 1, 0, 5, 6, 7, 8, 9 }
- 交换第一位和倒数第六位:{ 0, 2, 3, 1, 4, 5, 6, 7, 8, 9 }
- 保持二叉树 { 0, 2, 3, 1 } 的最大堆性质,得到新的数组:{ 3, 2, 0, 1, 4, 5, 6, 7, 8, 9 }
- 交换第一位和倒数第七位:{ 1, 2, 0, 3, 4, 5, 6, 7, 8, 9 }
- 保持二叉树 { 1, 2, 0 } 的最大堆性质,得到新的数组:{ 2, 1, 0, 3, 4, 5, 6, 7, 8, 9 }
- 交换第一位和倒数第八位:{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
- 保持二叉树 { 0, 1 } 的最大堆性质,得到新的数组:{ 1, 0, 2, 3, 4, 5, 6, 7, 8, 9 }
- 交换第一位和倒数第九位:{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
至此,整个堆排序过程结束。
6. 堆排序的时间复杂度
堆排序由两部分组成:
- 构建最大堆
- 循环保持最大堆的性质
6.1 构建最大堆的时间复杂度 T = O(n)
构建最大堆的过程,是从第一个非叶节点开始的,即数组的1/2处。
考虑最坏情况:
- 二叉树的倒数第二行,总会与最后一行发生一次比较/交换。
- 二叉树的倒数第三行,总会与倒数第二行发生一次比较/交换,与最后一行发生一次比较/交换。
- ...
- 二叉树的第一行,总会与它下面的每一行都发生一次比较/交换,即交换次数为二叉树高度 d=log2n。
将这些比较/交换次数累加:
T = () * n = O(n)
6.2 循环保持最大堆的性质的时间复杂度 T = O(n*log2n)
这一步的时间计算就相对比较明显了,在n次循环的内部,进行时间复杂度为 O(log2n) 的 maxHeapify()。
所以总时间复杂度 T = O(n) + O(n*log2n) = O(n*log2n)
Source Code: https://github.com/Gerrard-Feng/algorithm-learning.git