// 本文部分内容参照刘汝佳《算法竞赛入门经典训练指南》,特此说明。
[20190129更新!] 终于!时隔多年对这篇文章重新整理了一下,感谢大家提出的建议与意见。
1、前言
趁着这几天上午,把后缀数组大致看完了。这个东西本身的概念可能没太大理解问题,但是它所延伸出来的知识很复杂,很多,还有它的两个兄弟——后缀树,后缀自动机,编起来都不是盖的。
2、概念
前面曾经提到过AC自动机(http://www.cnblogs.com/jinkun113/p/4682853.html),讲得有点简略,它用以解决多模板匹配问题。但是前提是事先知道所有的模板,在实际应用中,我们无法事先知道查询内容的,比如在搜索引擎中,你的查询是不可能直接预处理出来的。这个时候就需要预处理文本串而非每次的查询内容。
后缀数组,说的简单一点,就是将一个字符串的所有后缀储存起来的数组,接下来分析它的作用。
3、构建
首先假定一个字符串BANANA,在后面添加一个非字母字符“$”,代表一个没出现过的标识字符,然后把它的所有后缀——

插入到一棵Trie中。由于标识字符的存在,字符串每一个后缀都与一个叶节点一一对应。如图所示:
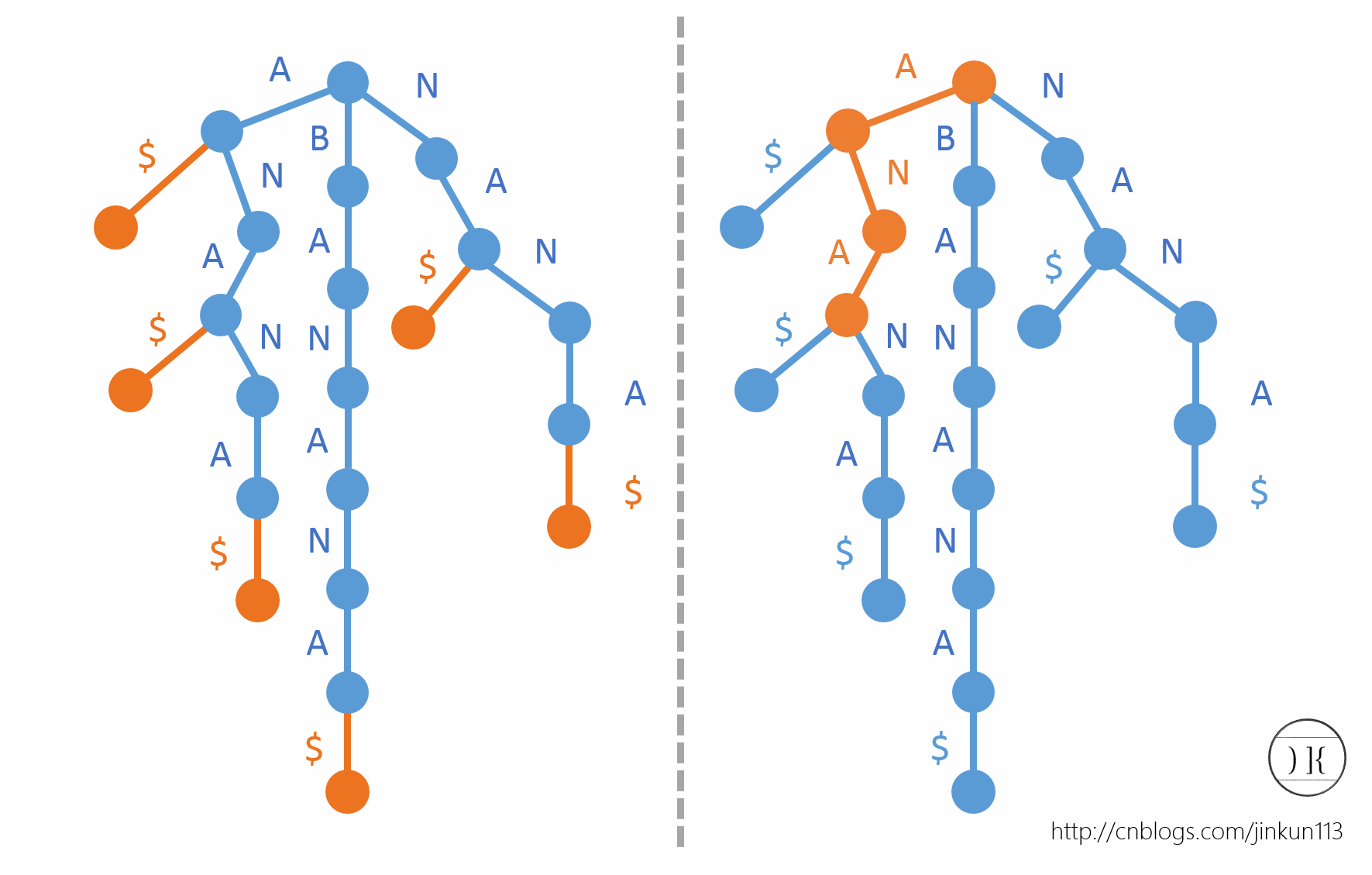
我们发现,有了后缀Trie之后,可以O(m)查找一个单词,如右侧。
在实际应用中,会把后缀Trie中没有分支的链合并在一起,得到所谓的后缀树,但是由于后缀树的构造算法复杂难懂,且容易写错,所以在竞赛中很少使用,所以暂时不去研究了。相比之下,后缀数组是必备武器,时间效率高,代码简单,而且不易写错。
在绘制后缀Trie的时候,我们将字典序小的字母排在左边。由于叶节点和后缀一一对应,我们现在在每一个叶节点上标上该后缀的首字母在原字符串中的位置,如图:
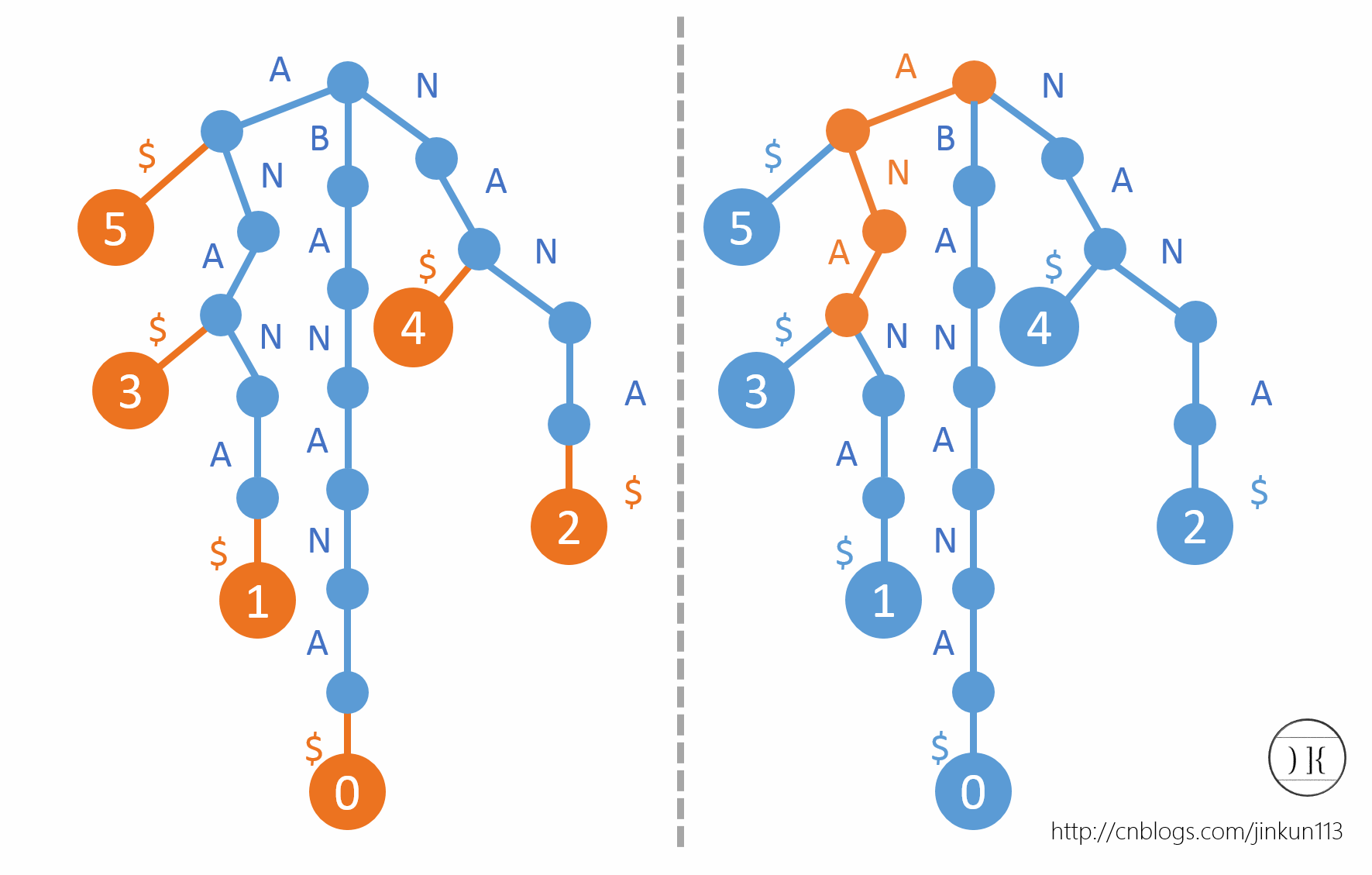
将所有下标连在一起,构建出来的,就是所谓的后缀数组了。BANANA的后缀数组为sa[] = {5, 3, 1, 0, 4, 2},举个例子,其中sa[1] = 3表示第3 + 1 = 4个字母开头的后缀即"ANA"在所有后缀中字典序排名为1。这样的话,我们就可以直接通过一次快速排序O(n log n)得到了。但是,在比较任意两个后缀时,又需要O(n),故这是O(n^2 log n),根本扛不住。
4、倍增
下面介绍Manber和Myers发明的倍增算法,时间复杂度O(n log n)(不采用基数排序的话就是O(n log^2 n))。
首先对于所有单个字符排序(也可以理解成对于每一个后缀的第1个字符排序,这样后面的步骤更易衔接),如图:
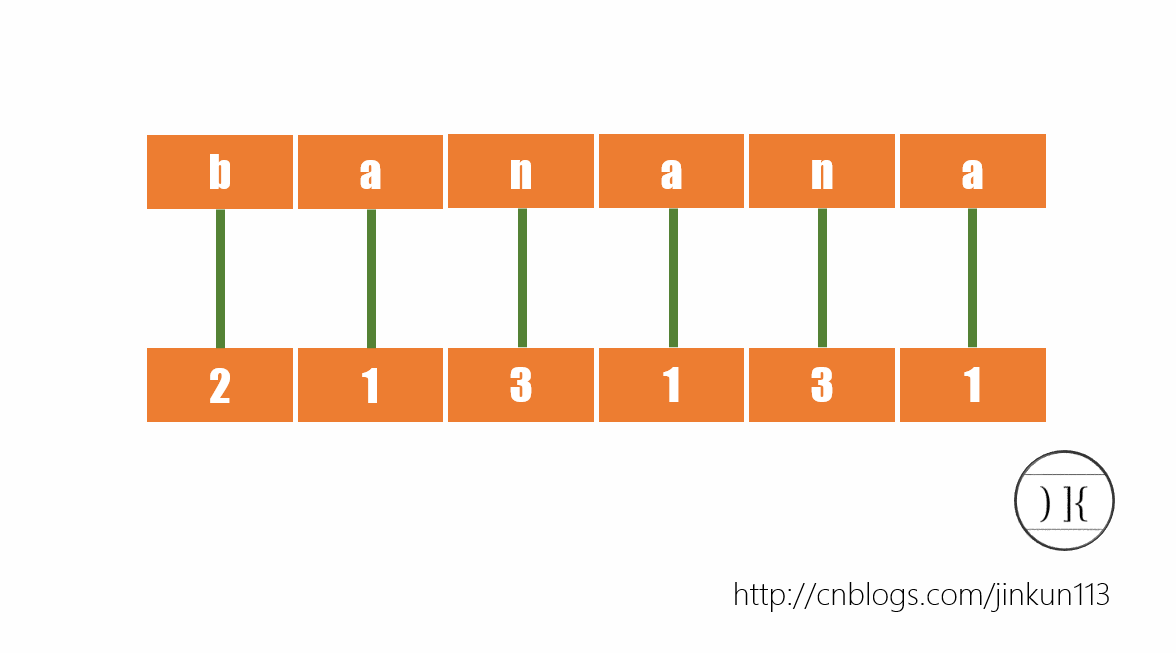
对于每个字母,我们根据字典序给予其一个名次,则a->1,b->2,n->3。
而接下来,我们再给所有后缀的前两个字符排序(之前就是前一个),将相邻二元组合并,再次根据字典序给予一个名次,如图:
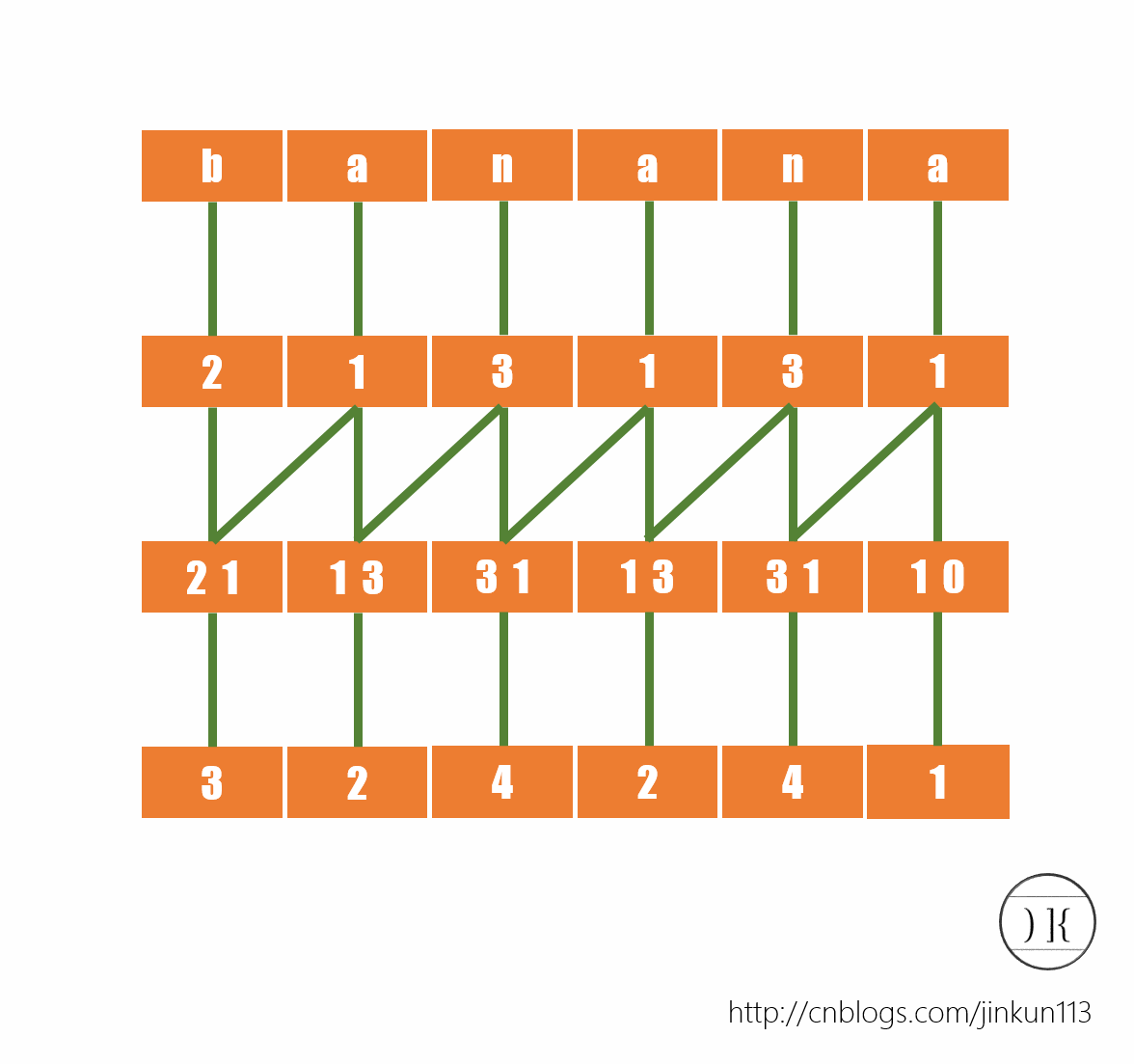
而我们现在得到了所有后缀的前2个字符的排名,注意这种方法是倍增思想,接下来要求的就是所有后缀的前4个字符的名次,因为可知对于后缀x的前4个字符是由后缀x的前2个字符和后缀x+2的前2个字符组成的,方法同上。如图:
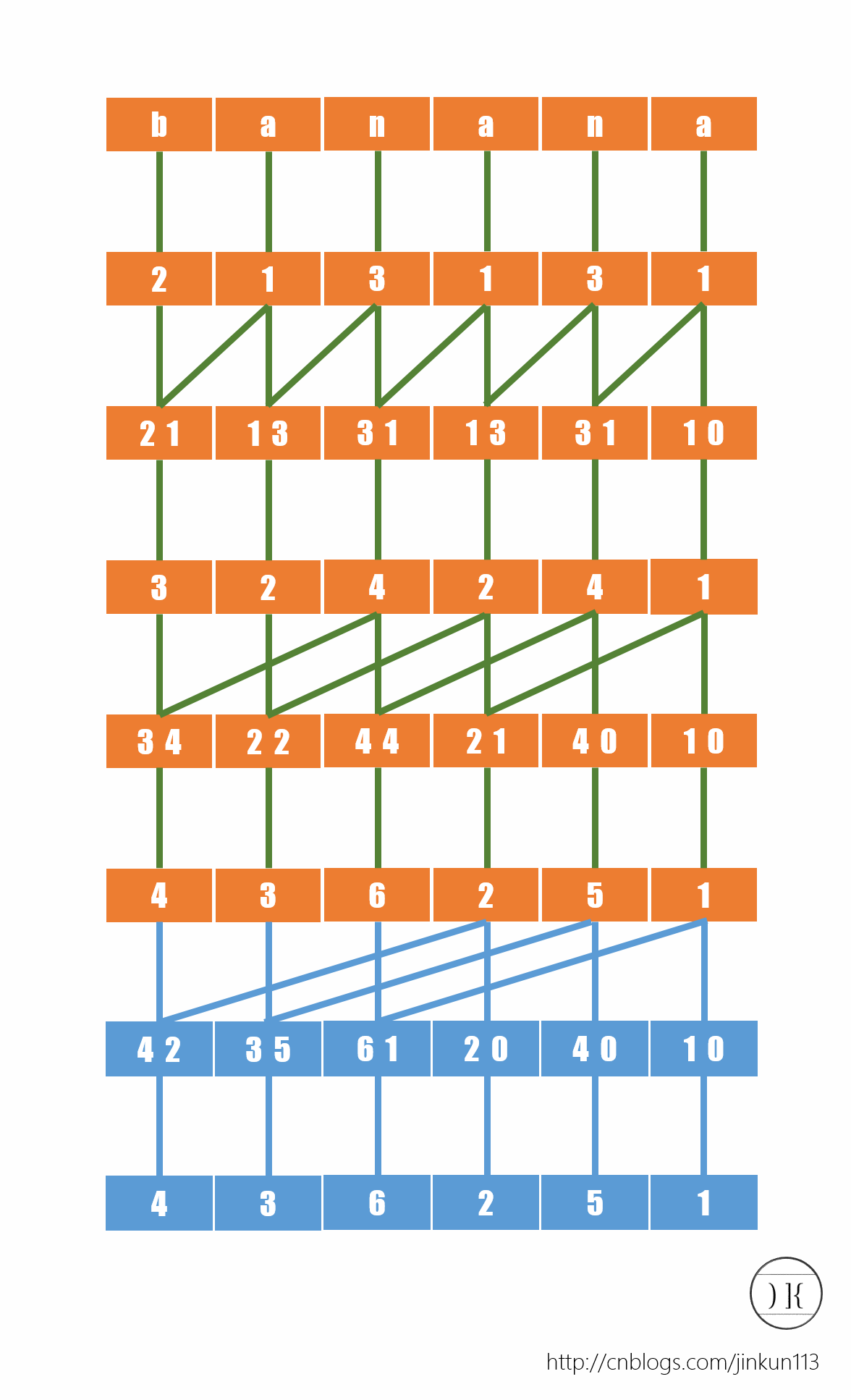
我们也可以注意到,当我们试图再去把所有后缀的前8个字符排一遍序的时候会发现,并没有任何含义。首先,这个字符串的长度没有达到8,其次所有名词已经两两不同,已经达到了我们的目的。所以我们可以分析出,这个过程的时间复杂度稳定为O(log n)。
得到了序列a[]={4,3,6,2,5,1},a[i]表示后缀i的名次。而后我们可以得到后缀数组了:sa[]={5,3,1,0,4,2}。(你要问我怎么得到的嘛?)
个人认为,这个思路自己想想还是好些,还是比较清晰的,起码我是先有思路再看懂网上文章的意思的。
5、基数排序
比较的复杂度为O(log n),如果这个时候再用快速排序的话,依旧需要O(n log^2 n),虽然已经小多了!但是,这个时候如果使用基数排序,可以进一步优化,达到O(n log n)。
首先先来介绍这个以前没听过的排序方法。设存在一序列{73,22,93,43,55,14,28,65,39,81},首先根据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中,如下图左侧所示:
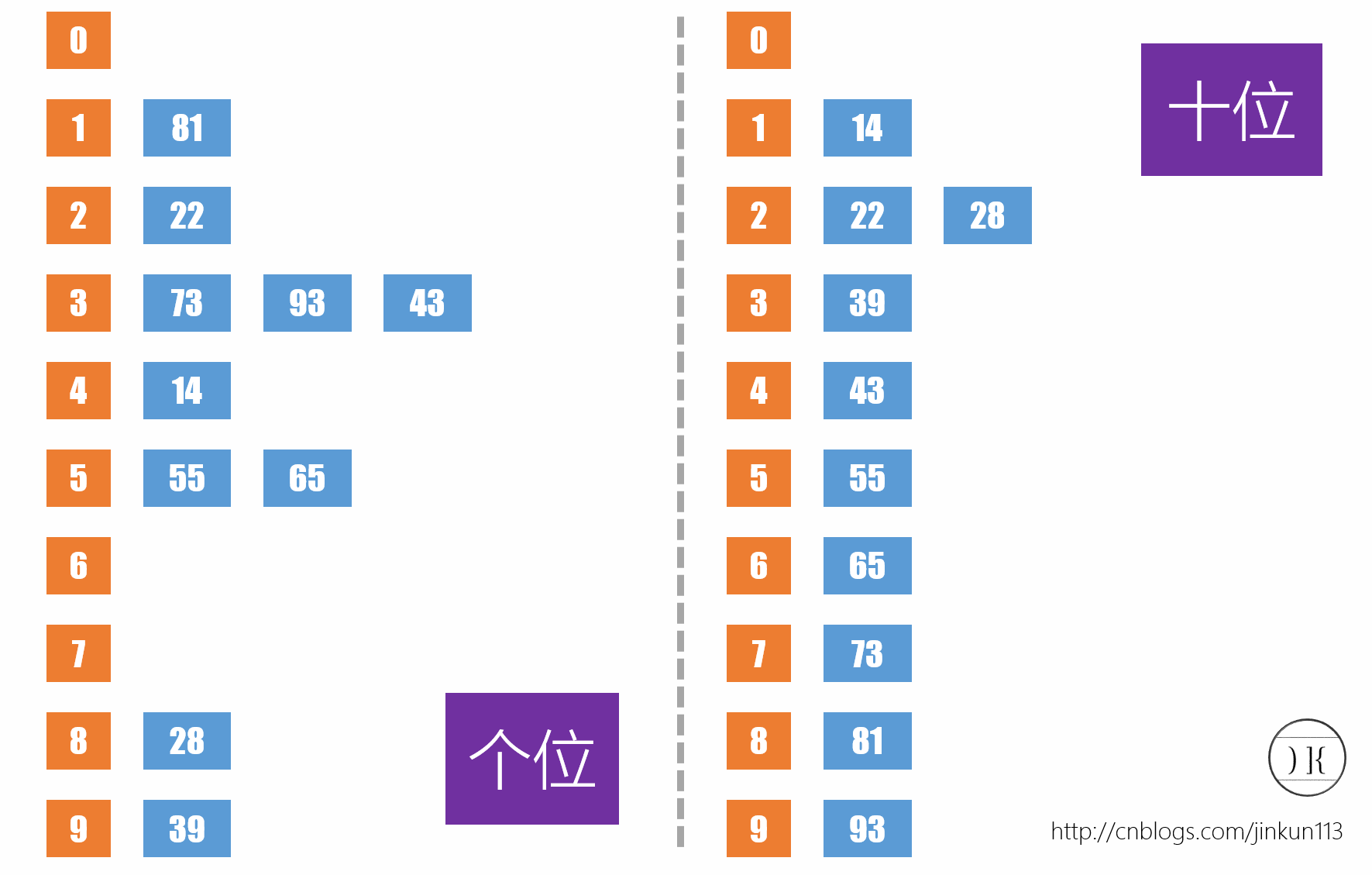
得到序列{81,22,73,93,43,14,55,65,28,39}。再根据十位数排序,如右侧,将他们连起来,得到序列{14,22,28,39,43,55,65,73,81,93}。
很好理解的一个排序。详细的内容不过多阐述。它的时间复杂度取决于数的多少以及数的位数。
在构建后缀数组的过程中,我们可以发现最大位数为2(字母总共只有26个),用基数排序的复杂度明显小于快速排序。下面给出一个临时的后缀数组构建模板,可以发现很多地方的模板都长这个样子的。
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 1005 5 #define MAXM 30 6 7 char ch[MAXN]; 8 int sa[MAXN], a[MAXN], t[MAXN], c[MAXN], n, m = MAXM, p; 9 10 int main() {
11 scanf("%s", ch), n = strlen(ch); 12 for (int i = 0; i < n; i++) c[a[i] = (ch[i] - 'a' + 1)]++; 13 for (int i = 1; i < m; i++) c[i] += c[i - 1]; 14 for (int i = n - 1; i >= 0; i--) 15 sa[--c[a[i]]] = i; 16 for (int k = 1; k <= n; k <<= 1) { 17 int p = 0; 18 for (int i = n - k; i < n; i++) t[p++] = i; 19 for (int i = 0; i < n; i++) if (sa[i] >= k) t[p++] = sa[i] - k; 20 for (int i = 0; i < m; i++) c[i] = 0; 21 for (int i = 0; i < n; i++) c[a[t[i]]]++; 22 for (int i = 0; i < m; i++) c[i] += c[i - 1]; 23 for (int i = n - 1; i >= 0; i--) sa[--c[a[t[i]]]] = t[i]; 24 swap(a, t); 25 p = 1, a[sa[0]] = 0; 26 for (int i = 1; i < n; i++) a[sa[i]] = (t[sa[i - 1]] == t[sa[i]] && t[sa[i - 1] + k] == t[sa[i] + k]) ? p - 1 : p++; 27 if (p >= n) break; 28 m = p; 29 } 30 return 0; 31 }
【对如上代码的注释】
n表示串的长度,m表示字符种类数。由于m没有直接给出,故初始赋值为30(大于可能出现的字符种类个数即可)。
6、最长公共前缀
目前我们得到的只有后缀数组一个东西。接下来就有一系列的延伸。比如说,在O(n log n)的时间内处理最长公共前缀,即LCP。求n个字符串LCP,暴力需要O(n^3),完全不是一个级别。
而利用后缀数组的话,通常需要两个数组,rank[i]表示后缀i在SA数组中的下标;height[i]表示sa[i-1]和sa[i]的最长公共前缀长度。对于两个前缀j和k,j<k,不妨设rank[j]<rank[k]。不难得到,后缀j和k的LCP长度等于height[rank[j+x]](x∈[1,k-j])中的最小值,举一个例子就能明白。

好还是好理解的,但是想想,根据定义,每次计算一对的height数组,都需要O(n),则共需要O(n^2),这显然让人感到不可忍,毕竟构建SA数组的时候都只需要O(n log n)。
然而这个时候我们再用个辅助数组a[i]=height[rank[i]],然后按照h[1],h[2]……h[n]的顺序递推计算。递推的关键在于这样一个性质:h[i]>=h[i-1]-1.这样就不需要从字符串开头计算了。如下方。
代码:
1 int rank[MAXN], height[MAXN]; 2 3 void geth() { 4 for (int i = 0; i < n; i++) rank[sa[i]] = i; 5 for (int i = 0; i < n; i++) { 6 if (k) k--; 7 int j = sa[rank[i] - 1]; 8 while (ch[i + k] == ch[j + k]) k++; 9 height[rank[i]] = k; 10 } 11 }
下面是该优化的证明:
设排在后缀i-1前一个的是后缀k。后缀k和后缀i-1分别删除首字符之后得到后缀k+1和后缀i,因此后缀k+1一定排在后缀i的前面,并且最长公共点缀长度为h[i-1]-1,如图所示:
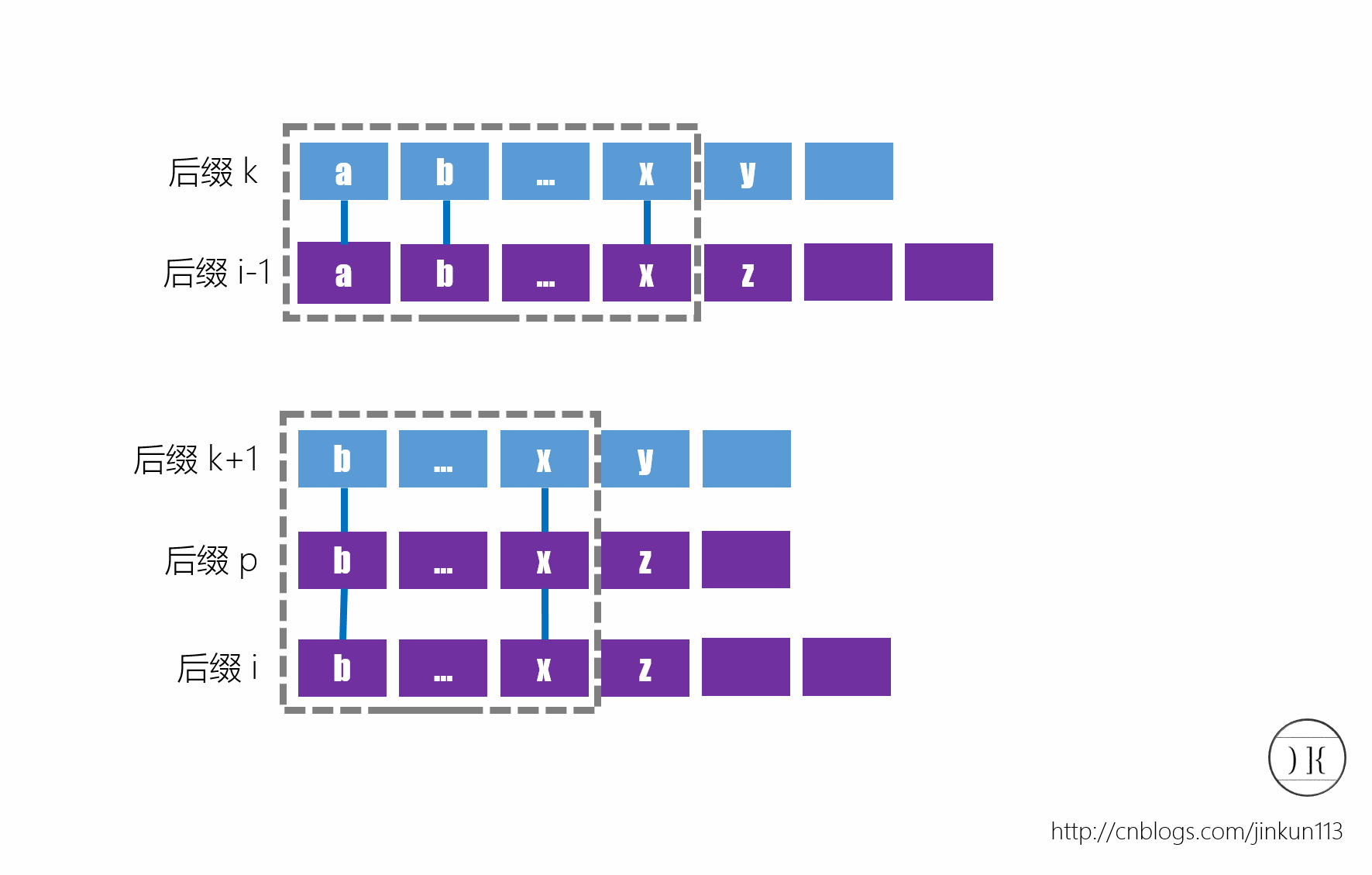
这个h[i-1]-1是一系列h值的最小值,这些h值包括后缀i和排在它前一个的后缀p的LCP长度,即h[i]。因此h[i]>=h[i-1]-1。
7、总结
这是一个非常高大上的东西,也许说这些看起来还是易懂的,但是题目做起来还是能够达到一种境界的。尤其还有后缀自动机等内容没有提。我认为后缀数组其实是个很巧妙的东西,更何况加在上面的各种优化。