线段树

线段树是一个用一个数组，想象一棵完全二叉树，赋予其一些意义，数组中存储的信息即为每个节点

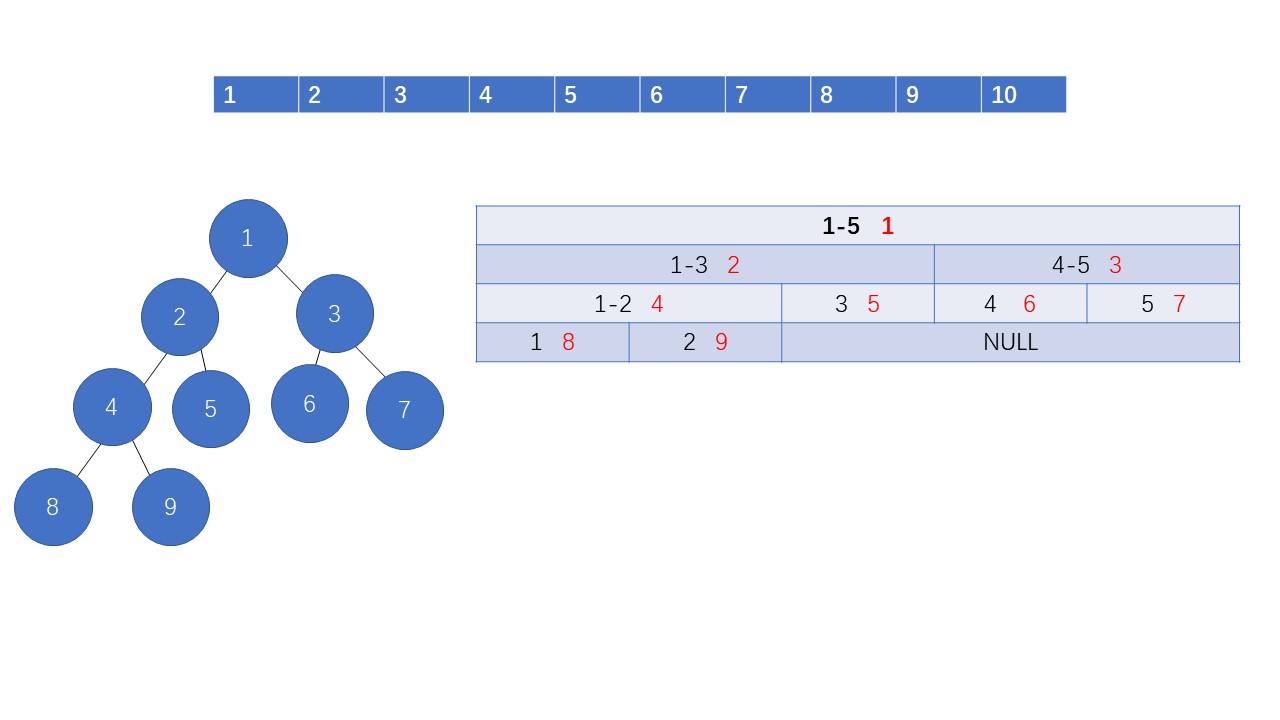
数组中的0 是不用的。

#define MAX 10000  //待处理的点数，不是树中的节点数
int tree[MAX * 4];
void build(int t, int l, int r)
{
    if (l == r)
    {
        //cin>>tree[t];
        //tree[t]=0;
        //对叶子初始化
        return;
    }
    int mid = l + r >> 1;
    build(t << 1, l, mid);
    build(t << 1 | 1, mid + 1, r);
    //tree[t] = tree[t << 1] + tree[t << 1 | 1];
    //tree[t] = max(tree[t << 1], tree[t << 1 | 1]);
    //对儿子节点递归完可以再用当前点的儿子更新当前点
}
//----------------------------------------------------------------------
void point_update(int t, int l, int r,int x,int y)//将a[x]改为y,点更新
{
    if (l == r)
    {
        //tree[t] = y;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)        //x在左边
        point_update(t << 1, l, mid, x, y);//继续将xy传参
    else if (x > mid)    //x在右边
        point_update(t << 1 | 1, mid + 1, r, x, y);
    //tree[t] = tree[t << 1] + tree[t << 1 | 1];
    //tree[t] = max(tree[t << 1], tree[t << 1 | 1]);
    //对儿子节点递归完可以再用当前点的儿子更新当前点
}
//-----------------------------------------------------------------------------------------
int ans;
void query(int t, int l, int r, int x, int y)//询问[x,y]的某东西，如最大值。区间查询,需要一个全局变量
{
    if (x <= l&&y >= r) //当前区间属于[x,y]
    {
        //ans += tree[t];
        return;
    }
    int mid = l + r >> 1;
    if (y <= mid)        //y<=mid说明整个查询区间都在左边
        query(t << 1, l, mid, x, y);//继续将xy传参
    else if (x > mid)    //x>mid说明整个查询区间都在右边
        query(t << 1 | 1, mid + 1, r, x, y);
    else                //区间跨过mid ，则分别往左右儿子递归
    {
        query(t << 1, l, mid, x, y);
        query(t << 1 | 1, mid + 1, r, x, y);
    }
}
//-------------------------------------------------------------------------
//区间更新还需要记录下每个节点打的标记
struct node
{
    int num;
    int flag;
}tre[MAX*4];
void interval_update(int t, int l, int r, int x, int y,int z)//[x,y]内的数都加z
{
    if (x <= l&&y >= r) //当前区间属于[x,y],不用再往下走，直接在这里打标记
    {
        tre[t].flag += z;
        return;
    }
    int mid = l + r >> 1;
    if (y <= mid)        //y<=mid说明整个查询区间都在左边
        interval_update(t << 1, l, mid, x, y,z);//继续将xy传参
    else if (x > mid)    //x>mid说明整个查询区间都在右边
        interval_update(t << 1 | 1, mid + 1, r, x, y,z);
    else                //区间跨过mid ，则分别往左右儿子递归
    {
        interval_update(t << 1, l, mid, x, y,z);
        interval_update(t << 1 | 1, mid + 1, r, x, y,z);
    }
}
void travel(int t, int l, int r, int f)//f为当前点所以祖先的flag之和
{
    if (l == r)
    {
        tre[t].num += f;
        tre[t].num += tre[t].flag;//应加上所有祖先的flag和自己的
        return;
    }
    int mid = l + r >> 1;
    travel(t << 1, l, mid,f+tre[t].flag);
    travel(t << 1 | 1, mid + 1, r,f+tre[t].flag);
    //tree[t] = tre[t << 1].num + tre[t << 1 | 1].num;
    //tree[t] = max(tre[t << 1].num, tre[t << 1 | 1].num);
    //对儿子节点递归完可以再用当前点的儿子更新当前点
}