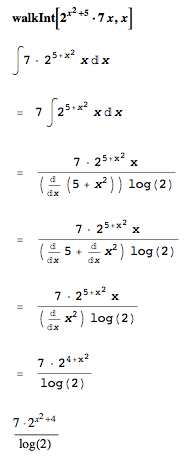Get a “step-by-step” evaluation in Mathematica

Is it possible in Mathematica to get a step-by-step evaluation of some functions; that's to say, outputting not only the result but all the stages that have led to it? If so, how does one do it?

----------------------------------------------------------------------------------

Here's  an attempt to (somewhat) modernize WalkD[]:

Format[d[f_, x_], TraditionalForm] := DisplayForm[RowBox[{FractionBox["[DifferentialD]",RowBox[{"[DifferentialD]", x}]], f}]];

SpecificRules = {d[x_, x_] :> 1, d[(f_)[x_], x_] :> D[f[x], x],
                 d[(a_)^(x_), x_] :> D[a^x, x] /; FreeQ[a, x]};

ConstantRule = d[c_, x_] :> 0 /; FreeQ[c, x];

LinearityRule = {d[f_ + g_, x_] :> d[f, x] + d[g, x],
                 d[c_ f_, x_] :> c d[f, x] /; FreeQ[c, x]};

PowerRule = {d[x_, x_] :> 1, d[(x_)^(a_), x_] :> a*x^(a - 1) /; FreeQ[a, x]};

ProductRule = d[f_ g_, x_] :> d[f, x] g + f d[g, x];

QuotientRule = d[(f_)/(g_), x_] :> (d[f, x]*g - f*d[g, x])/g^2;

InverseFunctionRule = d[InverseFunction[f_][x_], x_] :>1/Derivative[1][f][InverseFunction[f][x]];

ChainRule = {d[(f_)^(a_), x_] :> a*f^(a - 1)*d[f, x] /; FreeQ[a, x],
             d[(a_)^(f_), x_] :> Log[a]*a^f*d[f, x] /; FreeQ[a, x],
             d[(f_)[g_], x_] :> (D[f[x], x] /. x -> g)*d[g, x],
             d[(f_)^(g_), x_] :> f^g*d[g*Log[f], x]};

$RuleNames = {"Specific Rules", "Constant Rule", "Linearity Rule", "Power Rule","Product Rule", "Quotient Rule", "Inverse Function Rule", "Chain Rule"};

displayStart[expr_] := CellPrint[Cell[BoxData[MakeBoxes[HoldForm[expr], TraditionalForm]], "Output",Evaluatable -> False, CellMargins -> {{Inherited, Inherited}, {10, 10}},CellFrame -> False, CellEditDuplicate -> False]]

displayDerivative[expr_, k_Integer] := CellPrint[Cell[BoxData[TooltipBox[RowBox[{InterpretationBox["=", Sequence[]], "  ",MakeBoxes[HoldForm[expr], TraditionalForm]}], $RuleNames[[k]],LabelStyle -> "TextStyling"]], "Output", Evaluatable -> False,CellMargins -> {{Inherited, Inherited}, {10, 10}},CellFrame -> False, CellEditDuplicate -> False]]

WalkD[f_, x_] := Module[{derivative, oldderivative, k}, 
        derivative = d[f, x]; displayStart[derivative];While[! FreeQ[derivative, d],
            oldderivative = derivative; k = 0;While[oldderivative == derivative,
                      k++;
                      derivative = derivative /.ToExpression[StringReplace[$RuleNames[[k]], " " -> ""]]];
            displayDerivative[derivative, k]];D[f, x]]

I've tried to make the formatting of the derivative look a bit more traditional, as well as having the differentiation rule used be a tooltip instead of an explicitly generated cell (thus combining the best features of WalkD[] and RunD[]); you'll only see the name of the differentiation rule used if you mouseover the corresponding expression.

I have improved J. M.'s version of walkD by adding error handling. I have also added walkInt that works like walkD except for integration. Code:

Format[d[f_, x_], TraditionalForm] := Module[{paren, boxes},
    paren = MatchQ[f,Plus[_,__]];
    boxes = RowBox[{f}];If[paren,
        boxes = RowBox[{"(", boxes, ")"}]];
    boxes = RowBox[{FractionBox["[DifferentialD]", RowBox[{"[DifferentialD]", x}]], boxes}];DisplayForm[boxes]];

dSpecificRules = {d[x_, x_] :> 1, d[(f_)[x_], x_] :> D[f[x], x],
                 d[(a_)^(x_), x_] :> D[a^x, x] /; FreeQ[a, x]};

dConstantRule = d[c_, x_] :> 0 /; FreeQ[c, x];

dLinearityRule = {d[f_ + g_, x_] :> d[f, x] + d[g, x],
                 d[c_ f_, x_] :> c d[f, x] /; FreeQ[c, x]};

dPowerRule = {d[x_, x_] :> 1, d[(x_)^(a_), x_] :> a*x^(a - 1) /; FreeQ[a, x]};

dProductRule = d[f_ g_, x_] :> d[f, x] g + f d[g, x];

dQuotientRule = d[(f_)/(g_), x_] :> (d[f, x]*g - f*d[g, x])/g^2;

dInverseFunctionRule := d[InverseFunction[f_][x_], x_] :>1/Derivative[1][f][InverseFunction[f][x]];

dChainRule = {d[(f_)^(a_), x_] :> a*f^(a - 1)*d[f, x] /; FreeQ[a, x],
             d[(a_)^(f_), x_] :> Log[a]*a^f*d[f, x] /; FreeQ[a, x],
             d[(f_)[g_], x_] :> (D[f[x], x] /. x -> g)*d[g, x],
             d[(f_)^(g_), x_] :> f^g*d[g*Log[f], x]};

$dRuleNames = {"Specific Rules", "Constant Rule", "Linearity Rule", "Power Rule","Quotient Rule", "Product Rule", "Inverse Function Rule", "Chain Rule"};

displayStart[expr_] := CellPrint[Cell[BoxData[MakeBoxes[HoldForm[expr], TraditionalForm]], "Output",Evaluatable -> False, CellMargins -> {{Inherited, Inherited}, {10, 10}},CellFrame -> False, CellEditDuplicate -> False]];

displayDerivative[expr_, k_Integer] := CellPrint[Cell[BoxData[TooltipBox[RowBox[{InterpretationBox["=", Sequence[]], "  ",MakeBoxes[HoldForm[expr], TraditionalForm]}], "Differentation: " <> $dRuleNames[[k]],LabelStyle -> "TextStyling"]], "Output", Evaluatable -> False,CellMargins -> {{Inherited, Inherited}, {10, 10}},CellFrame -> False, CellEditDuplicate -> False]];walkD::differentationError = "Failed to differentiate expression!";

walkD[f_, x_] := Module[{derivative, oldderivative, k}, 
    derivative = d[f, x]; displayStart[derivative];While[! FreeQ[derivative, d],
        oldderivative = derivative; k = 0;While[oldderivative == derivative,
            k++;If[k > Length@$dRuleNames,Message[walkD::differentationError];Return[D[f, x]];];
    			derivative = derivative /. ToExpression["d" <> StringReplace[$dRuleNames[[k]], " " -> ""]]];
        displayDerivative[derivative, k]];D[f, x]];Format[int[f_,x_],TraditionalForm]:= (
    paren = MatchQ[f,Plus[_,__]];
    boxes = RowBox[{f}];If[paren,
        boxes = RowBox[{"(", boxes, ")"}]];
    boxes = RowBox[{boxes, "[DifferentialD]", x}];
    boxes = RowBox[{"[Integral]", boxes}];DisplayForm[boxes]);

intSpecificRules = {int[(f_)[x_], x_] :> Integrate[f[x], x],
                   int[(a_)^(x_), x_] :> Integrate[a^x, x] /; FreeQ[a, x]};

intConstantRule = int[c_, x_] :> c*x /; FreeQ[c, x];

intLinearityRule = {int[f_ + g_, x_] :> int[f, x] + int[g, x],
                   int[c_ f_, x_] :> c int[f, x] /; FreeQ[c, x]};

intPowerRule = {int[x_, x_] :> x^2 / 2, int[1/x_, x_] :> Log[x], int[(x_)^(a_), x_] :> x^(a + 1)/(a + 1) /; FreeQ[a, x]};

intSubstitutionRule = {
                        int[(f_)^(a_), x_] :> ((Integrate[u^a, u] / d[f, x]) /. u -> f) /; FreeQ[a, x] && FreeQ[D[f, x], x],
                        int[(f_)^(a_) g_, x_] :> ((Integrate[u^a, u] / d[f, x]) * g /. u -> f) /; FreeQ[a, x] && FreeQ[FullSimplify[D[f, x] / g], x],
                        int[(a_)^(f_), x_] :> (a ^ f)/(d[f, x] * Log[a]) /; FreeQ[a, x] && FreeQ[D[f, x], x],
                        int[(a_)^(f_) g_, x_] :> (a ^ f)/(d[f, x] * Log[a]) * g /; FreeQ[a, x] && FreeQ[FullSimplify[D[f, x] / g], x],
                        int[(f_)[g_], x_] :> (Integrate[f[u], u] /. u -> g) / d[g, x] /; FreeQ[D[g, x], x],
                        int[(f_)[g_] h_, x_] :> (Integrate[f[u], u] /. u -> g) / d[g, x] * h /; FreeQ[FullSimplify[D[g, x] / h], x]};

intProductRule = int[f_ g_, x_] :> int[f, x] g - int[int[f, x] * d[g, x], x];

$intRuleNames = {"Specific Rules", "Constant Rule", "Linearity Rule", "Power Rule", "Substitution Rule", "Product Rule"};

displayIntegral[expr_, k_Integer] := CellPrint[Cell[BoxData[TooltipBox[RowBox[{InterpretationBox["=", Sequence[]], "  ",MakeBoxes[HoldForm[expr], TraditionalForm]}], "Integration: " <> $intRuleNames[[k]],LabelStyle -> "TextStyling"]], "Output", Evaluatable -> False,CellMargins -> {{Inherited, Inherited}, {10, 10}},CellFrame -> False, CellEditDuplicate -> False]];walkInt::integrationError = "Failed to integrate expression!";walkInt::differentationError = "Failed to differentiate expression!";

walkInt[f_, x_] := Module[{integral, oldintegral, k, leafcounts, ruleused},
    integral = int[f, x]; displayStart[integral];
    leafcounts = {};
    ruleused = "";While[! FreeQ[integral, int],If[ruleused == "Product Rule",AppendTo[leafcounts, LeafCount @ integral];If[Length @ leafcounts >= 5 && OrderedQ @ Take[leafcounts, -5],Message[walkInt::integrationError];Return[Integrate[f, x]];];];
        oldintegral = integral; k = 0;While[oldintegral == integral,
            k++;If[k > Length@$intRuleNames,Message[walkInt::integrationError];Return[Integrate[f, x]];];
    			integral = integral /. ToExpression["int" <> StringReplace[$intRuleNames[[k]], " " -> ""]]];
        ruleused = $intRuleNames[[k]];
    		displayIntegral[integral, k];While[! FreeQ[integral, d],
    			oldintegral = integral; k = 0;While[oldintegral == integral,
    				k++;If[k > Length@$dRuleNames,Message[walkInt::differentationError];Return[Integrate[f, x]];];
                integral = integral /. ToExpression["d" <> StringReplace[$dRuleNames[[k]], " " -> ""]]];
            displayDerivative[integral, k]];];Integrate[f, x]];

Sample output:

来源： http://mathematica.stackexchange.com/questions/148/get-a-step-by-step-evaluation-in-mathematica

来自为知笔记(Wiz)