[编程题] lc [69. x 的平方根]

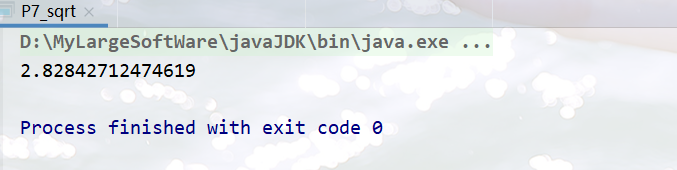
[编程题] 69. x 的平方根

题目

方法1：二分法

Java代码

public static int sqrt(int x) {
        if(x==0 || x==1){return x;}
        int l=0;
        int  r=x;
        int res=-1;
        while (l<=r){
            int m = (l+r)/2;
            if(m == x/m) {
                return m;
            }
            else if(m>x/m) {
                r = m-1;
            } else{
                l = m+1;
                res = m;  //解释：为什么时刻在这里记录m是因为我们舍弃了小数部分，只有m*m<x的情况符合我们需要的m
            }
        }
        return res;
}

方法2：牛顿迭代法

公式推导

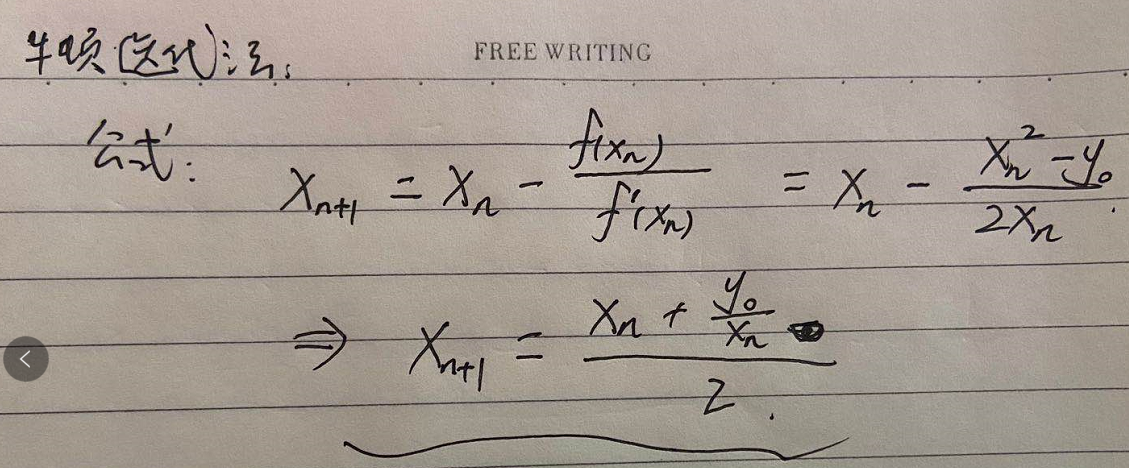
代码

//根据牛顿迭代法公式：x(n+1) = (xn+y0/xn)/2
public static int mySqrt3(int x) {  //如果我们要精确计算值也可以把返回值改为double即可
    long r = x; //r*r会越界，这里用long
    while (r*r>x){
        r = (r+x/r)/2;
    }
    return (int)r;
}

---

我们计算出需要的指定精度的确切值

方法1：二分法

public static double sqrt2(int x) {
        if(x==0 || x==1){return x;}
        double l=0;
        double r=x;

        double res=-1;
        while (r-l>=1e-9){  ////这里是精度判断的退出条件
            double m = (l+r)/2;
            if(m == x/m) {
                return m;
            }
            else if(m>x/m) {
                r = m-1e-9;  //这里是每次减去精度
            } else{
                l = m+1e-9; //这里是每次减去精度 
                res = m;  //解释：为什么时刻在这里记录m是因为我们舍弃了部分精确值，只有m*m<x的情况符合我们需要的m
            }
        }
        return res;
}

方法2：牛顿迭代法

//根据牛顿迭代法公式：x(n+1) = (xn+y0/xn)/2
    public static double sqrt3(int x) {
        double r = x;
        while (r*r>x){
            r = (r+x/r)/2;
        }
        return r;
}