[编程题] 基础 【动态规划】与练习-爬楼梯
知识点
1、基础

2、斐波那契数列例子
普通递归:
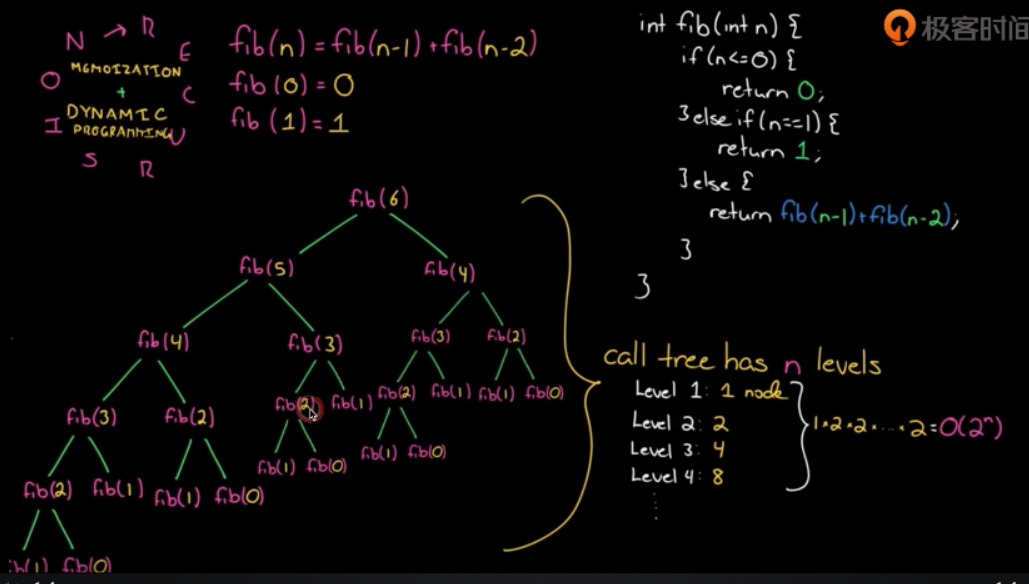
递归加记忆化

那么从树的下边往上推的话,顺推上去没救得到了状态转移方法。

案例1:爬楼梯
回溯的方法
回溯的思想是,我们如果是想到达第n台阶f(n)的话,那么就是从f(n-1)跳上来,也可以是从f(n-2)跳上来。即
f(n) = f(n-1) + f(n-2)
f(0) = f(1) = 1
动态规划
for(int i=2;i<n;i++){
f[n] = f[n-1] + f[n-2];
}
总结:动态规划dp转移方程状态定义;dp转移方程
Java办法的几种代码
import java.util.*;
class Solution {
//方法1:递归:(时间超过限制)
public int climbStairs1(int n) {
//方法1:普通递归的方法进行
if(n==1 ||n==2) {
return n;
}else{
return climbStairs(n-1)+climbStairs(n-2);
}
}
//方法2:动态规划(空间换时间)
public int climbStairs2(int n) {
if(n<=2){return n;}
//n>=3的情况使用dp处理
int[] dp = new int[n+1];
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<=n;i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
//方法3:滑动数组的方式(从左往右滑)
public int climbStairs3(int n) {
int p = 0; //pre节点指针
int q = 1; //相当于n=1的情况的指针
int r = 2; //相当于n=2的情况的指针
for(int i=1;i<n;i++){ //传入2,只需要移动1次,传入3,只需移动2次
p = q;
q = r;
r = p+q;
}
return q;
}
//方法4:使用斐波那契公式计算
public int climbStairs6(int n) {
double sqrt5 = Math.sqrt(5);
int res = (int)((1/sqrt5)*(Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1)));
return res;
}
}