[编程题]【动态规划】背包问题
参考这个大神讲解的背包问题后自己写的代码,up主讲的太清楚了
题目信息
问题:现有背包。其中有四个商品。价值-体积如下
* 物品编号: 1 2 3 4
* 物品体积: 2 3 4 5
* 物品价值: 3 4 5 6
* 问:如何才能保证在背包容量为8的情况下装的价值最大?
思路
背包问题,动态规划
思路
1、构建dp表,dp【i】【j】代表该i编号的背包为止容量为j的最大价值。先填表加深理解。
2、填完表如果要找出价值为k的容量的背包加入的物品标号只需要从i=dp.length-1,j=k的dp数组元素处回溯。
填完表如下(借视频中up主的结果):
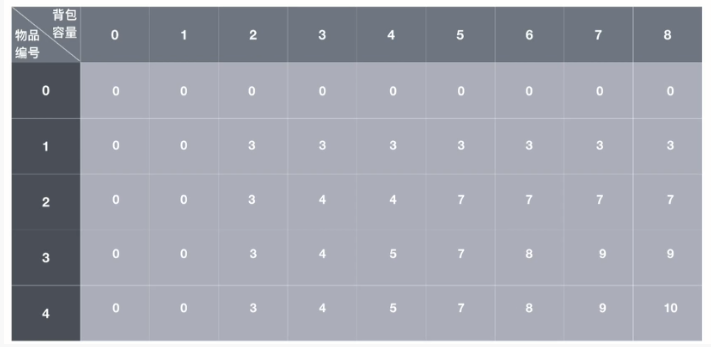
总结结论如下(借视频中up主的总结):

理解了上述总结的思路,其实代码就很容易写出来了。
代码如下
Java代码
package interviewcode;
import java.lang.annotation.Target;
import java.util.ArrayList;
import java.util.Arrays;
/**
* @author
* @create 2020/8/11 - 10:52
* @descp:
* 问题:现有背包。其中有四个商品。价值体积如下
* 物品编号: 1 2 3 4
* 物品体积: 2 3 4 5
* 物品价值: 3 4 5 6
* 问:如何才能保证在背包容量为8的情况下装的价值最大?
*
* 步骤1:填表之后的结果:
* 0 0 0 0 0 0 0 0 0
* 0 0 3 3 3 3 3 3 3
* 0 0 3 4 4 7 7 7 7
* 0 0 3 4 5 7 8 9 9
* 0 0 3 4 5 7 8 9 10
* 步骤2:回溯
*/
//方法:动态规划
public class P28_背包问题 {
public static void main(String[] args) {
int[] size = new int[]{0,2,3,4,5}; //第0位放一个默认的0值,为了下边方便取size[i]就为i号物品的体积
int[] money = {0,3, 4, 5, 6}; //第0位放一个默认的0值,为了下边方便取money[i]就为i号物品的价值
int target = 14; //指定的背包大小
//调用
int[][] ints = dpWrite(size, money, target);
ArrayList<Integer> huisu = huisu(ints, size, target);
System.out.println("您输入的背包大小是:"+target);
System.out.println("添加的物品编号是:"+huisu);
System.out.println("最大价值:"+ints[size.length-1][target]);
}
public static int[][] dpWrite(int[] size,int[] money,int targetValue){
//这里构造一个例如4*8的dp,行代表截止到i背包的最优组合的价值,j代表的背包的容量值
int[][] dp = new int[size.length][targetValue+1];
//初始化第0行的值
for(int j=0;j<=targetValue;j++){
dp[0][j] = 0;
}
//初始化第一列的值
for(int i=1;i<size.length;i++){
dp[i][0] = 0;
//dp[i][1] = 0;
}
//初始化中间值i
for(int i=1;i<size.length;i++){
for (int j=1;j<=targetValue;j++){
//如果第i号背包的体积小于当前的j背包容量,就保持和dp[i-1]值相同,即没放入
if(size[i]>j){
dp[i][j] = dp[i-1][j];
}else{
/*即如果当前i号物品体积可以放入的话,就看预留该体积后剩余的价值在i-1号物品中的最大值加上该物品的价值和是否
是大于dp[i-1][j]的值,谁大取谁*/
dp[i][j] = Math.max(dp[i-1][j-size[i]>0?j-size[i]:0]+money[i],dp[i-1][j]);
}
}
}
//这样就填表完成了。剩下的就是需要回溯取出看对应某价值target的物品组合是什么
//先打印一下填的表
/*for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[i].length; j++) {
System.out.print(dp[i][j]+" ");
}
System.out.println();
}*/
return dp;
}
public static ArrayList<Integer> huisu(int[][] dp,int[] size, int t){
ArrayList<Integer> res = new ArrayList<>();
int i = dp.length-1;
int j = t;
while (i>0 || j>0){
if(dp[i][j]==dp[i-1][j]){
i--;
}else{
res.add(i);
j = j-size[i];
i--;
}
}
return res;
}
}
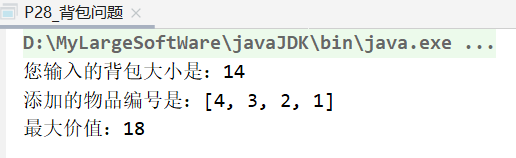
输出:
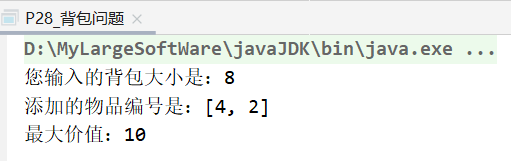
测试1:例如:背包容量8,输出物品编号和可以获得的最大价值:
测试2:例如:背包容量14,输出物品编号和可以获得的最大价值: