一、递归原理小案例分析
(1)# 概述
递归:即一个函数调用了自身,即实现了递归 凡是循环能做到的事,递归一般都能做到!
(2)# 写递归的过程
1、写出临界条件
2、找出这一次和上一次关系
3、假设当前函数已经能用,调用自身计算上一次的结果,再求出本次的结果
(3)案例分析:求1+2+3+...+n的数和
# 概述 ''' 递归:即一个函数调用了自身,即实现了递归 凡是循环能做到的事,递归一般都能做到! ''' # 写递归的过程 ''' 1、写出临界条件 2、找出这一次和上一次关系 3、假设当前函数已经能用,调用自身计算上一次的结果,再求出本次的结果 ''' # 问题:输入一个大于1 的数,求1+2+3+.... def sum(n): if n==1: return 1 else: return n+sum(n-1) n=input("请输入:") print("输出的和是:",sum(int(n))) ''' 输出: 请输入:4 输出的和是: 10 '''

#__author:"吉*佳" #date: 2018/10/21 0021 #function: import os def getAllDir(path): fileList = os.listdir(path) print(fileList) for fileName in fileList: fileAbsPath = os.path.join(path,fileName) if os.path.isdir(fileAbsPath): print("$$目录$$:",fileName) getAllDir(fileAbsPath) else: print("**普通文件!**",fileName) # print(fileList) pass getAllDir("G:\")
输出结果如下:


二、深度遍历与广度遍历
(一)、深度优先搜索
说明:深度优先搜索借助栈结构来进行模拟
深度遍历示意图:
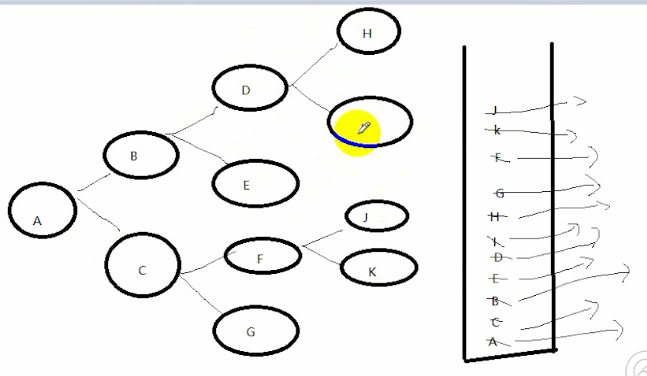
说明:
先把A压栈进去,在A出栈的同时把B C压栈进去,此时让B出栈的同时把DE压栈(C留着先不处理) 同理,在D出栈的时候,H I压栈,最后再从上往下
取出栈内还未出栈的元素,即达到深度优先遍历。
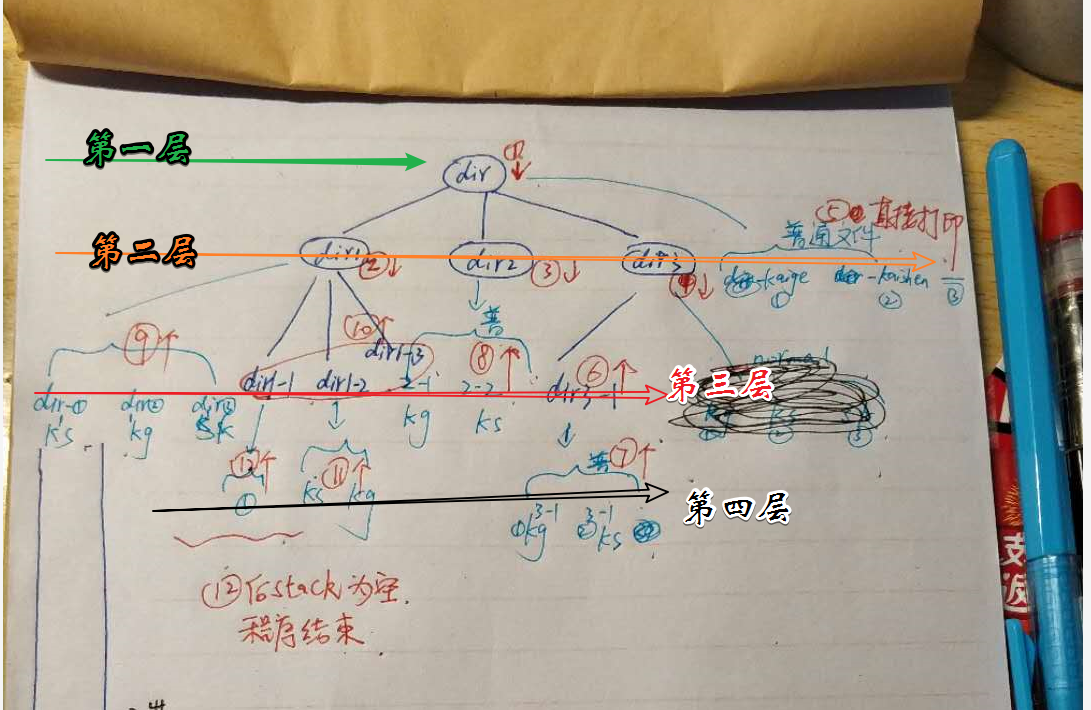
案例实践:利用栈来深度搜索打印出目录结构

程序代码:
#__author:"吉**" #date: 2018/10/21 0021 #function: # 深度优先遍历目录层级结构 import os def getAllDirDP(path): stack = [] # 压栈操作,相当于图中的A压入 stack.append(path) # 处理栈,当栈为空的时候结束循环 while len(stack) != 0: #从栈里取数据,相当于取出A,取出A的同时把BC压入 dirPath = stack.pop() firstList = os.listdir(dirPath) #判断:是目录压栈,把该目录地址压栈,不是目录即是普通文件,打印 for filename in firstList: fileAbsPath=os.path.join(dirPath,filename) if os.path.isdir(fileAbsPath): #是目录就压栈 print("目录:",filename) stack.append(fileAbsPath) else: #是普通文件就打印即可,不压栈 print("普通文件:",filename) getAllDirDP(r'E:[AAA](千)全栈学习python18-10-21day7 empdir')
结果:

该过程示意图解释:(s-05-1部分)
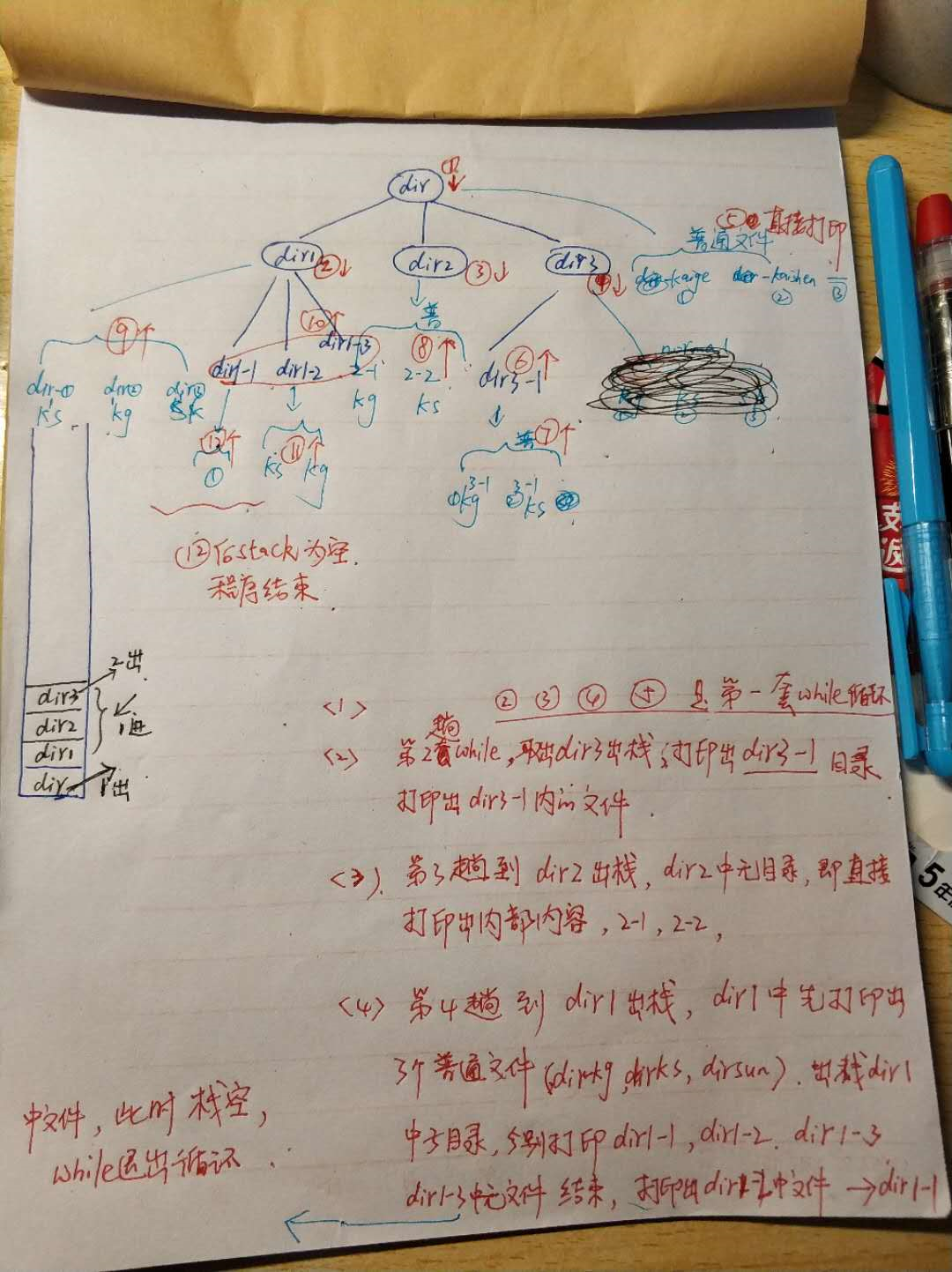

原理分析:

说明:
队列是 先进先出的模型。A先进队,在A出队的时候,C B入队,按图示,C出队,FG 入队,B出队,DE入队,
F出队,JK入队,G出队,无入队,D出队,H I入队,最后E J K H I出队,均无入队了,即每一层一层处理、
故:先进先出的队列结构实现了广度优先遍历。 先进后出的栈结构实现的是深度优先遍历。
代码实现:
其实深度优先和广度优先在代码书写上是差别不大的,基本相同,只是一个是使用栈结构(用列表进行模拟)
另一个(广度优先遍历)是使用了队列的数据结构来达到先进先出的目的。
#__author:"吉**" #date: 2018/10/21 0021 #function: # 广度优先搜索模拟 # 利用队列来模拟广度优先搜索 import os import collections def getAllDirIT(path): queue=collections.deque() #进队 queue.append(path) #循环,当队列为空,停止循环 while len(queue) != 0: #出队数据 这里相当于找到A元素的绝对路径 dirPath = queue.popleft() # 找出跟目录下的所有的子目录信息,或者是跟目录下的文件信息 dirList = os.listdir(dirPath) #遍历该文件夹下的其他信息 for filename in dirList: #绝对路径 dirAbsPath = os.path.join(dirPath,filename) # 判断:如果是目录dir入队操作,如果不是dir打印出即可 if os.path.isdir(dirAbsPath): print("目录:"+filename) queue.append(dirAbsPath) else: print("普通文件:"+filename) # 函数的调用 getAllDirIT(r'E:[AAA](千)全栈学习python18-10-21day7 empdir')
广度优先运行输出结构:
先图解:按照每一层从左到右遍历即可实现。