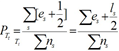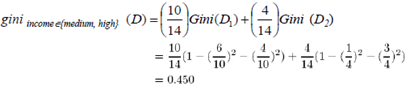一、决策树学习(适用于“属性-值”实例且输出值离散)
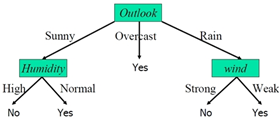
决策树学习是一种逼近离散值目标函数的方法,这个方法学到的函数称为一棵决策树。学到的决策树可表示为多个if-then过程以提高可读性。主要算法有:ID3、ASSISTANT、C4.5。决策树的节点表示某个属性,每个分支对应一个属性值,叶子结点为实例所属的分类,整个决策树是实例属性值的合取析取式。图例如下:
该决策树的表达式:
二、ID3算法(每次选信息增益最大的属性)
ID3算法步骤:
a.对当前例子集合,计算各属性的信息增益
b.选择信息增益最大的属性Ai
c.在Ai处取相同值的例子归于同一个子集,Ai取几个值就得几个子集
d.依次对每种取值情况下的子集,递归调用建树算法,即返回步骤a
e.若子集的class目标属性相同,则分支为叶子节点,并标上class标签,然后返回调用处。
信息增益Gain(S,A)表示A带来的信息量(熵降低),v∈Values(A)中v是属性A的某个可能值,Sv为该属性值的集合:
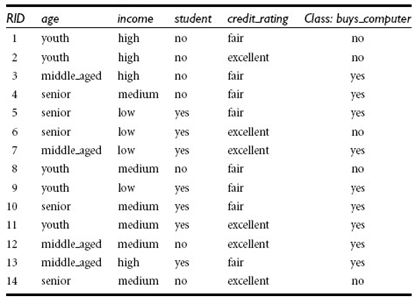
[例]决策是否买了电脑,训练数据如下:
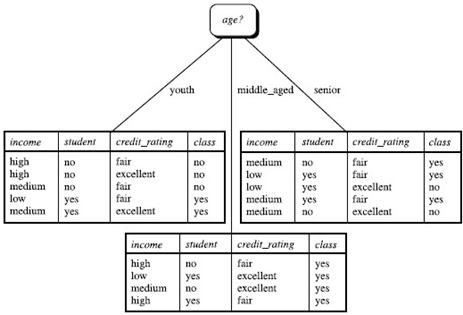
其中Gain(age)=0.94-[(5/14)*0.971+(4/14)*0+(5/14)*0.971)=0.246>Gain(student)=0.151>Gain(income)=0.029的信息增益,因此选择age属性。从age节点开始继续迭代选择信息增益最大的属性,直到分到某类时class标签一致为止。
三、C4.5算法(ID3的改进算法)
C4.5算法继承了ID3算法的优点,并在以下几方面对ID3算法进行了改进:用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值较多属性的不足;在树构造过程中进行剪枝;能够完成对连续属性的离散化处理;能够对不完整数据进行处理。
C4.5算法步骤:
a. 读取文件信息,统计数目
b. 建立决策树
如果样本集为空,则生成一个信息数目都为0的树节点返回
如果样本均为同一类别,则生成一个叶子节点返回
计算节点正负样本的数目
如果属性值只有那个类别的属性,则生成一个叶子节点,并赋值类型标签索引
如果以上都不是,则选择一个信息增益率最大的属性(连续属性要用增益率离散化),按那个属性的取值情况从新定义样本集和属性集,建造相关子树
c. 事后剪枝(采用悲观错误率估算)
d. 输出决策树
e. 移除决策时
算法核心:1.计算信息增益率;2.悲观错误率剪枝;3.分治思想构造树
1.信息增益率
GainRatio(income)=0.029/0.926=0.031
2.悲观错误率剪枝(将错误率较大的子树剪掉)
悲观错误率:
假设s为树T的子树t的其中一个子节点,则该子树t的叶子结点个数为ls,Tt的分类错误率为:
定性可用错误总数代替,上式化为:
三、Gini Index基尼系数(用于IBM的IntelligentMiner,寻找最小的Gini分割系数)
定义Gini系数如下:
若将数据分成两个子集,则分割后的Gini系数为:
提供最小的Ginisplit就被选为分割的标准。
[例]是否已买电脑,其中9yes,5no。
假设income属性的Gini分割系数为: