链接
https://www.acwing.com/problem/content/description/346/
题目
给定一张无向图,求图中一个至少包含3个点的环,环上的节点不重复,并且环上的边的长度之和最小。
该问题称为无向图的最小环问题。
你需要输出最小环的方案,若最小环不唯一,输出任意一个均可。
输入格式
第一行包含两个整数N和M,表示无向图有N个点,M条边。
接下来M行,每行包含三个整数u,v,l,表示点u和点v之间有一条边,边长为l。
输出格式
输出占一行,包含最小环的所有节点(按顺序输出),如果不存在则输出’No solution.’。
数据范围
1≤N≤100,
1≤M≤10000,
1≤l<500
输入样例:
5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20
输出样例:
1 3 5 2
思路
首先要清楚flody算法的原理
f[k][i][j]表示从i到j中间路径点编号(不包括i,j)的最大值是k的最短路。
用集合的角度来分析,形如这样的环,i-k,k-j是边,i-j是路径,这样保证了是环,且环上的点数至少是3,只要考虑了所有点对以及所有点对经过的中间点,就不会有遗漏:
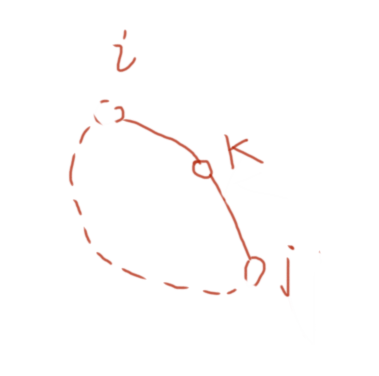
k表示如上环中的最大节点编号k(注意不是路径),通过确定i,j来考虑第k类。

所以在求解的过程中,从小到大枚举k,在k没有考虑进任何(i,j)点对之间的最短路之前去计算如上图的环,求出环之后再将k考虑进i-j的最短路环中。
最后用分治的思想去求环上的点。
需要注意的是,求环的过程中:
for(int k=1;k<=n;++k)
for(int i=1;i<k;++i)
for(int j=i+1;j<k;++j)
if((LL)g[i][k]+g[k][j]+d[j][i]<circled)
和
for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(i!=j&&j!=k&&i!=k&&(LL)g[i][k]+g[k][j]+d[j][i]<circled)
都是正确的写法。但是flody不能按照第一个代码那样写。因为求环只考虑了包含i-k-j这两条边的最小环,而foldy考虑的是一条路径。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
typedef long long LL;
int g[N][N],d[N][N];
int pos[N][N],cnt;
int path[N];
void get_path(int l,int r){
if(l==0||r==0) return ;
get_path(l,pos[l][r]);
if(pos[l][r])
path[++cnt]=pos[l][r];
get_path(pos[l][r],r);
}
int main(){
int n,m;
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--){
int x,y,z;
cin>>x>>y>>z;
g[x][y]=g[y][x]=min(g[x][y],z);
}
for(int i=1;i<=n;++i) g[i][i]=0,pos[i][i]=i;
memcpy(d,g,sizeof d);
int circled=0x3f3f3f3f;
for(int k=1;k<=n;++k){
for(int i=1;i<k;++i){
for(int j=i+1;j<k;++j){
if((LL)g[i][k]+g[k][j]+d[j][i]<circled){
circled=g[i][k]+g[k][j]+d[j][i];
cnt=0;
path[++cnt]=i;
get_path(i,j);
path[++cnt]=j;
path[++cnt]=k;
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(d[i][j]>(LL)d[i][k]+d[k][j]){
d[i][j]=d[i][k]+d[k][j];
pos[i][j]=k;
}
}
}
}
if(circled==0x3f3f3f3f)puts("No solution.");
else {
for(int i=1;i<=cnt;++i) cout<<path[i]<<" ";
}
return 0;
}