Luogu 3246 序列
- 考虑莫队,不算特别优秀,但足以通过此题.
- 用莫队做,先考虑在当前区间右边加入一个数对答案的影响,其他三种情况同理.
- 若加入新数的区间为 ([L,R]) ,那么加的贡献就是 ([L,R],[L+1,R]dots [R,R]) 这些区间最小值之和.
- 用单调栈预处理出每个数 (a_i) 左边第一个比它小的数的位置 (sl) ,那么它被记作最小值的区间就是 ([sl+1,R],[sl+2,R]dots[i,R]) ,被算了 (i-sl) 次.那么就这样一个个往前面跳,类似于树的结构.
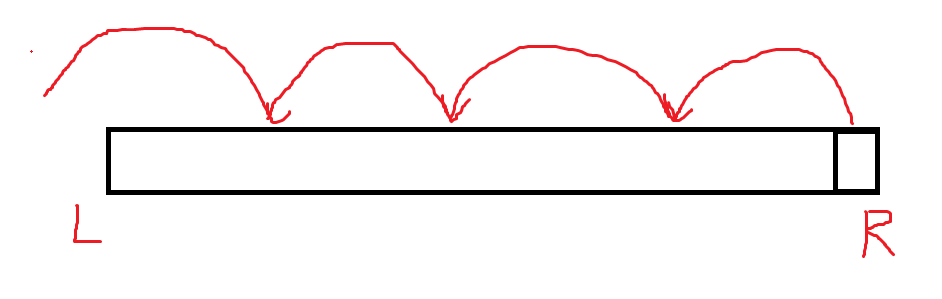
- 这个东西显然可以在算完 (sl) 后立刻求出,算一下前缀和,那么每次查询也是 (O(1)) 的.
- 注意到最前面那个元素会跳出去,被算的次数不是 (i-sl) ,而是 (i-L+1),需要单独算.按照定义,它显然是 ([L,R]) 这个区间内的最小值,用 (ST) 表问一下位置,大小就可以了.
写这个题又复习了一遍莫队...询问排序第一关键字是左端点的块,第二关键字是右端点...另外,那四个 (while) 移动端点的顺序不能乱写...不然会出现 (L>R) 的尴尬情况..如果样例没测出来这题可就爆零了...
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read()
{
int out=0,fh=1;
char jp=getchar();
while ((jp>'9'||jp<'0')&&jp!='-')
jp=getchar();
if (jp=='-')
fh=-1,jp=getchar();
while (jp>='0'&&jp<='9')
out=out*10+jp-'0',jp=getchar();
return out*fh;
}
const int MAXN=1e5+10;
struct query
{
int l,r,bel,id;
bool operator < (const query &rhs) const
{
if(bel!=rhs.bel)
return bel<rhs.bel;
if(r!=rhs.r)
return r<rhs.r;
return l<rhs.l;
}
} q[MAXN];
int a[MAXN];
int st[MAXN][18],stp[MAXN][18];
int n,Q;
int sl[MAXN],sr[MAXN];
int stk[MAXN],stkpos[MAXN],tp;
ll suml[MAXN],sumr[MAXN];
ll res,ans[MAXN];
int mi,pos;
inline void st_init()
{
for(int i=1;i<=n;++i)
st[i][0]=a[i],stp[i][0]=i;
for(int j=1;(1<<j)<=n;++j)
for(int i=1;i+(1<<j)-1<=n;++i)
{
if(st[i][j-1]<st[i+(1<<(j-1))][j-1])
st[i][j]=st[i][j-1],stp[i][j]=stp[i][j-1];
else
st[i][j]=st[i+(1<<(j-1))][j-1],stp[i][j]=stp[i+(1<<(j-1))][j-1];
}
}
void query(int l,int r)
{
int k=log(r-l+1)/log(2.0);
if(st[l][k]<st[r-(1<<k)+1][k])
mi=st[l][k],pos=stp[l][k];
else
mi=st[r-(1<<k)+1][k],pos=stp[r-(1<<k)+1][k];
}
void addl(int L,int R)
{
query(L,R);
ll delta=1LL*(R-pos+1)*mi;
delta+=sumr[L]-sumr[pos];
res+=delta;
}
void reml(int L,int R)
{
query(L,R);
ll delta=1LL*(R-pos+1)*mi;
delta+=sumr[L]-sumr[pos];
res-=delta;
}
void addr(int L,int R)
{
query(L,R);
ll delta=1LL*(pos-L+1)*mi;
delta+=suml[R]-suml[pos];
res+=delta;
}
void remr(int L,int R)
{
query(L,R);
ll delta=1LL*(pos-L+1)*mi;
delta+=suml[R]-suml[pos];
res-=delta;
}
void init()
{
st_init();
stk[++tp]=0;
stkpos[tp]=0;
for(int i=1; i<=n; ++i)
{
while(tp)
{
if(a[i]<=stk[tp])
--tp;
else
break;
}
sl[i]=stkpos[tp];
stk[++tp]=a[i];
stkpos[tp]=i;
suml[i]=suml[sl[i]]+1LL*(i-sl[i])*a[i];
}
tp=0;
stk[++tp]=0;
stkpos[tp]=n+1;
for(int i=n; i>=1; --i)
{
while(tp)
{
if(a[i]<=stk[tp])
--tp;
else
break;
}
sr[i]=stkpos[tp];
stk[++tp]=a[i];
stkpos[tp]=i;
sumr[i]=sumr[sr[i]]+1LL*(sr[i]-i)*a[i];
}
}
int main()
{
n=read(),Q=read();
int Blocksize=sqrt(Q);
for(int i=1; i<=n; ++i)
a[i]=read();
for(int i=1; i<=Q; ++i)
{
q[i].l=read();
q[i].r=read();
q[i].bel=q[i].l/Blocksize;
q[i].id=i;
}
sort(q+1,q+1+Q);
init();
int L=1,R=0;
for(int i=1; i<=Q; ++i)
{
int l=q[i].l,r=q[i].r;
while(R<r)
addr(L,++R);
while(L<l)
reml(L++,R);
while(L>l)
addl(--L,R);
while(R>r)
remr(L,R--);
ans[q[i].id]=res;
}
for(int i=1; i<=Q; ++i)
printf("%lld
",ans[i]);
return 0;
}