计算机思维-符号化计算化与自动化

0-1 与 易经的关系

语义符号化->符号计算化->计算0-1化->0-1自动化 -> 分层构造化 -> 构造集成化

• 理解-区分-命名
  术语很重要, 通过术语区分概念
  自然现象抽象为符号组合, 变成0-1组合, 0/1组合的变换/基于0/1的计算在语义化就可以得到自然规律的变化
  符号-->组合--->命名--->本体/用体

• 0-1的逻辑
  逻辑是指事物因果之间的所遵循的规律, 是现实社会中普世的思维方式
  逻辑的基础是命题和推理
  例如: 再一次考试中, 三位老师做了预测, A有人及格, B有人不及格 C全班都不及格
  考试后只有一个老师预测是正确的,请问是哪个老师?
  推出 A是真

• 基本逻辑运算
  与 运算 X与Y都为真, AandY为真, 其他都是假
  或 运算 X与Y都为假, AorY 为假, 其他都为真
  非 运算, 相反 X为真 结果为假
  异或运算 XOR, 相同时候结果为假, 不同时候为真
  

• 0-1 数值型信息
  数位的权值, 不同的数位代表不同的数值
  
  为什么用二进制呢?

1. 是运算规则比较简单, 只有0-1
2. 是可以与逻辑运算统一起来, 元器件比较容易实现
3. 不同进制都可以转化为十进制
   通常O表示八进制, OX或者H表示十六进制
   同一个数值, 用不同的进位制表示出来是不同的

• 数值的正负号处理
  正数 原码符号位为0 正数的原码反码 和补码都是一样的
  负数 原码符号位为1, 反码是原码的位数取反, 补码是反码的基础上加1
  为什么用补码表示?
  用其他方式需要符号位, 暂用了一个位数, 而补码不管是正数还是负数都是一样的, 这样可以表示的数位就多一位.
  用补码符号也可以参与运算, 不会影响. 原码表示减法可以用加法表示
  
  小数点的处理, 定点数和浮点数
  定点数-->小数点的位置是固定的
  浮点数--> 小数点的位置不是固定的, 把小数存储类似于科学计数法, 有指数部分和尾数部分
  小数的位数不同, 分为单精点数是32位(指数8位, 尾数23位), 双精点数是64位(11位,尾数53)
  运算规则与整数不同, 需要一个协处理器参与运算
• 信息的度量单位
  bit 一个二进制位0/1
  Byte 字节 8个二进制位
  1Kb 市场约1024字节
• 非数值信息可以用编码表示
  编码是人为的将若干位数码或者符号的不同组合, 表示一个非数值信息,例如 0---男, 1---女
  编码的三个特征:

1. 唯一性, 每一种组合都有一个确定的信息
2. 公共性: 所有使用者都认同和遵守, 使用这种编码
3. 易于记忆/便于认识 有一定的规律, 这个不重要了, 因为不是人阅读的, 是给机器阅读的
   ASCII吗 26个大小写英文字母, 128个数字即可, 1个字节就可以表示ASCII吗
   ASCII吗有一些规律:
   41H-5AH : "A"-"Z"
   61H-7AH: 'a' - 'z'
   比如: 信息 We are students 可以存储为一串0-1字符, 按照8位分隔一个字符, 查询ASCII表映射成相应的符号
   
   数字 0 0
   字符 0 00010010
   我们在程序设计中, 为什么要定义变量的类型, 就是不同的类型暂用的空间是不一样的, 对应的解码方式也是不一样的, 解析还原的时候也是不一样的, 所以我们在使用的时候要注意变量的类型
   汉字的编码
   汉字编码--- 需要两个字节来表示一个汉字
   
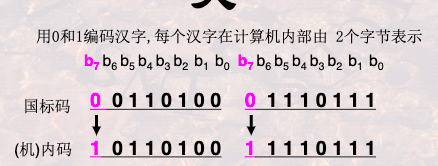
   为了与ASCII进行区分,我们把两个最高位变为1, 当我们在读取0-1串的时候, 如果我们发现最高位是1, 这就是一个汉字编码
   汉字怎么输入到计算机内部?
   
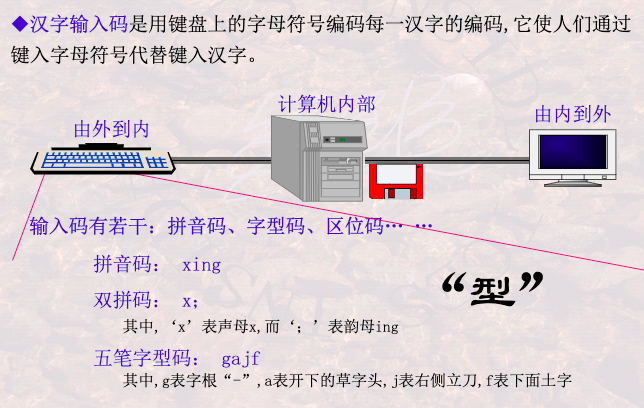
   汉字的显示
   

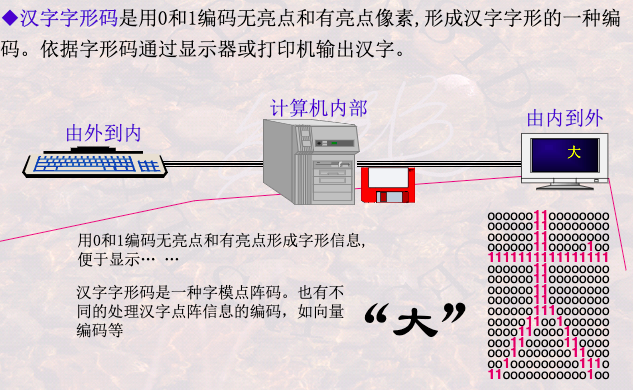
• 汉字的处理过程
  
  之前对这些东西都学了, 但是不太理解, 今天学了一次, 真是大彻大悟, 很爽
• 0-1 与电子技术实现
  如何用电信号来表示0-1?
  用数字信号: 高电平为1 低电平为0
  也可以使用继电器开关, 实现基本逻辑运算
  
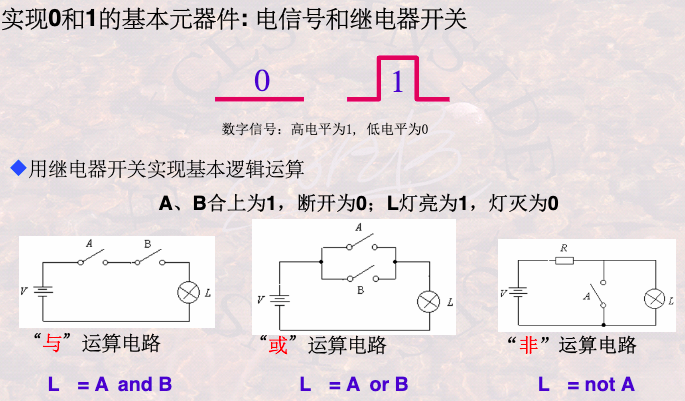
  0-1, 与或非都是可以使用电路进行表示
  
  这些都是用三极管实现出来, 然后封装就可以做出一个运算,
  
  这样加减乘除都是可以表示为加法, 同样对于每一个逻辑运算又可以做成一个加集成电路
  
  
  为什么使用与或非门? 使用与或非门的效率更高
  
  底层的电路验证是正确的, 我们八个或者16个封装起来, 就可以做高位的运算, 就是分层构造的思想, 先将基础的功能实现, 然后在封装出更高层的功能
  2-4 译码器