2020-12-7 翻转矩阵后的得分

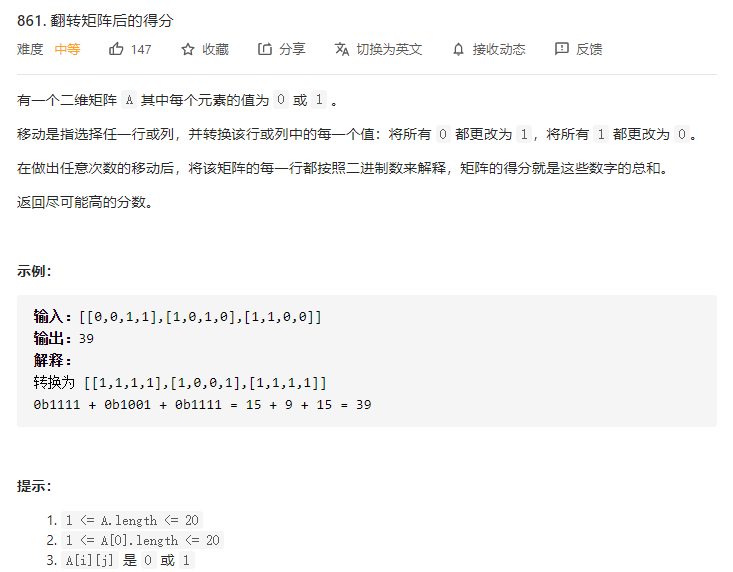
题目

解题思路

本题的目标是通过多次行或列的反转，以使得数组中各行所表示的二进制数的值之和最大。
经分析可知，要使和最大，须优先使得列下标值较小的列中1的个数最多。所以得到如下思路：

1. 通过行反转使得第一列的所有元素均为1（即每行的第一个元素均为1）
2. 然后遍历除第一列外的每一列，求出每列中1的个数，若其小于行数的一半，便对该列进行反转。
3. 最后对得到的最佳矩阵求和。

代码实现

class Solution {
public:
    int matrixScore(vector<vector<int>>& A) {
        vector<int> cnt(A[0].size()-1, 0);

        // 使每行的第一个元素都变为1
        for (int i = 0; i < A.size(); i++){
            if (A[i][0] == 0)
                reverseArr(A[i]);
        } 

        // 遍历除第一列外的元素，记录各列为1的个数保存入数组cnt
        for (int j = 1; j < A[0].size(); j++){
            for (int i = 0; i < A.size(); i++){
                if (A[i][j] == 1)
                    cnt[j-1]++;
            }
			
            if (cnt[j-1] < A.size()/2+1){
                for (int i = 0; i < A.size(); i++){
                    A[i][j] ^= 1; 
                }
                cnt[j-1] = A.size() - cnt[j-1];
            }
        }

        // 求和
        int sum = A.size() * pow(2, A[0].size()-1);
        for (int i = 1; i < A[0].size(); i++)
            sum += cnt[i-1] * pow(2, A[0].size()-i-1);
    
        return sum;
    }

    void reverseArr(vector<int>& arr){
        for (int i = 0; i < arr.size(); i++)
            arr[i] ^= 1;
    }
};

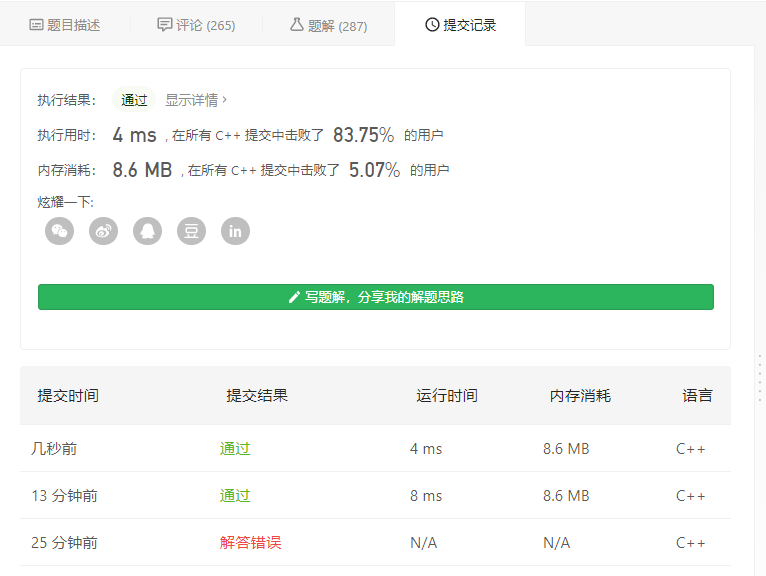
提交结果