解法一:快速排序,时间O(nlog(n)),额外空间O(1),但是有两个样例会超时。
(土法分析)快速排序在有序的情况下时间复杂度O(n2)最高,而没有通过的样例估算约为50001个1和50000个2,因此O(n2)的复杂度约为10^10,某大佬说过,根据经验,超过10^9 OJ一般就不会通过,因此快排不行,因为人家特意准备了样例;因此解法2尝试了归并排序保证最坏情况下可以ac;
class Solution { public: int majorityElement(vector<int>& nums) { QuickSort(nums,0,nums.size()-1); int candidate=NULL; int count=0; for(int i=0;i<nums.size();i++){ if(candidate==nums[i]) count++; else{ count=1; candidate=nums[i]; } if(count>nums.size()/2) return candidate; } return 0; } int partition(vector<int>& nums,int low,int high){ int pivotkey=nums[low]; while(low<high){ while(low<high && nums[high]>=pivotkey){ high--; } nums[low]=nums[high]; while(low<high && nums[low]<=pivotkey){ low++; } nums[high]=nums[low]; } nums[low]=pivotkey; return low; } void QuickSort(vector<int>& nums,int low,int high){ if(low>=high) return; int pivot=partition(nums,low,high); QuickSort(nums,low,pivot-1); QuickSort(nums,pivot+1,high); } };
解法2:使用归并排序,可以ac,时间O(nlog(n)),然后空间O(n+log(n))栈的深度,额外空间为递归栈的深度log(n);
class Solution { public: int majorityElement(vector<int>& nums) { mergesort(nums,0,nums.size()-1); return nums[nums.size()/2]; } void merge(vector<int> & nums,int left,int mid,int right){ vector<int> temp; int l=left,r=mid+1; while(l<=mid && r<=right){ if(nums[l]<nums[r]) temp.push_back(nums[l++]); else temp.push_back(nums[r++]); } while(l<=mid){ temp.push_back(nums[l++]); } while(r<=right){ temp.push_back(nums[r++]); } for(int i=0;i<right-left+1;i++){ nums[left+i]=temp[i]; } } void mergesort(vector<int> &nums,int left, int right){ if(left>=right) return; int mid=(right+left)/2; mergesort(nums,left,mid); mergesort(nums,mid+1,right); merge(nums,left,mid,right); } };
解法三:使用关联容器map,unordered_map,multiset,来count超过半数的数,额外空间O(n),时间O(n)
class Solution { public: int majorityElement(vector<int>& nums) { map<int,int> m; for(int n:nums){ if(m.count(n)>0) m[n]++; else m[n]=1; } for(int n:nums){ if(m[n]>nums.size()/2) return n; } return 0; } };
解法四:神仙方法摩尔投票 时间O(n)空间O(1)大概是最好的办法;
有个博主解释的很好我就不重复了mark下当做以后复习的材料https://blog.csdn.net/qq_17550379/article/details/83818965这位博主是python代码我用c++重写了一遍
本质上是用cnt模拟了栈,所以也可以用栈写;

class Solution { public: int majorityElement(vector<int>& nums) { int cnt=0,key=nums[0]; for(int n:nums){ if(cnt==0) key=n; if(key==n) cnt++; else cnt--; } return key; } };
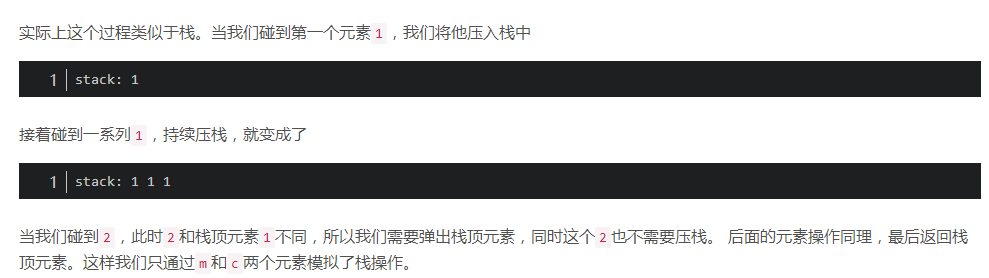
用栈实现求众数,这个时间O(n),空间大概O(n)最坏因为当全是同一个数时栈是n;
class Solution { public: int majorityElement(vector<int>& nums) { stack<int> st; for(int n:nums){ if(st.empty() || st.top()==n) st.push(n); else st.pop(); } return st.top(); } };