减而治之

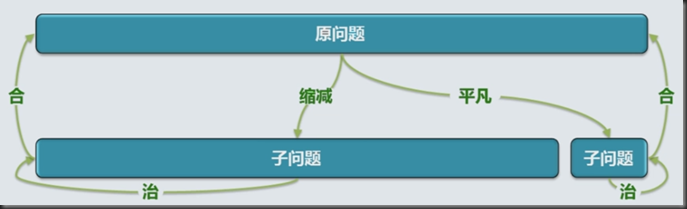
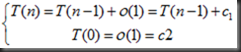• 复杂度分析：
• • ：线性时间复杂度
  • ，其中，则称为“多项式时间复杂度算法”
  • • 多项式时间复杂度被视作一个具有特殊意义的复杂度级别：多项式的运行时间成本，在实际应用中一般被认为是可接受的
    • 若问题存在一个复杂度在此范围以内的算法，则称该问题是可有效求解的或易解的
  • ：指数时间复杂度算法
  • • 问题规模较大后，指数复杂度算法的实际效率将急剧下降，无法正在应用于实际问题中，即不是有效算法
• 复杂度层次：

• 递归
• • 线性递归：每一层次上至多只有一个实例，且它们构成一个线性的次序关系
  • • 减而治之：递归每深入一层，待求解的问题的规模都缩减一个常数，直至最终蜕化为平凡的小问题

• 递归分析
  • 数组求和的递归形式：

int sum(int []a,  n){

    if ( 1 > n) {

        return  0;

    }

    else {

        return A[n-1] + sum(a, n-1);

    }

}

• • 递归跟踪：

               按照以下规则，将递归算法的执行过程整理为图的形式：

• • • 算法的每一递归实例都表示为一个方框，其中注明了该实例调用的参数
    • 若实例N调用实例M，则在 N、M对应的方框之间添加一条有向联线

               按上述方法，递归求和的算法过程如下：

• • • 时间复杂度 = 递归实例的调用次数 * 每个递归实例的时间消耗 = 递归实例的调用次数 * （递归实例的创建、执行、销毁），又递归实例的创建、销毁、调用有操作系统完成，可近似为常数，即

                              时间复杂度 = 递归实例的调用次数 * （递归实例的执行） =

• • • 空间复杂度 = 递归实例的调用次数 * 每个递归实例的空间消耗 =
  • 递推方程：通过对递归模式的数学归纳，导出复杂度定界函数的递推方程（组）及其边界条件，从而将复杂度的分析，转化为递归方程（组）的求解
  • • 递推方程：

• • • 时间复杂度：
    • 空间复杂度：