梯度是微积分多元函数的一个重要概念,简单来说,梯度是一个向量,当函数上的一点按照该向量移动,函数值增加最大,该向量由函数分别对自变量的偏导值所构成。如果函数是二元函数,则梯度是二维向量,在自变量构成的平面上,如果函数是三元函数,则梯度是三维向量,在自变量构成的空间中。本文着重对它的上述的意义,进行形象的阐述。
下面分别举个例子:
(1)u(x,y)=x**2+y**2,在(-10,10)这一点,梯度向量为(-20,-20)。
其图像如下图:
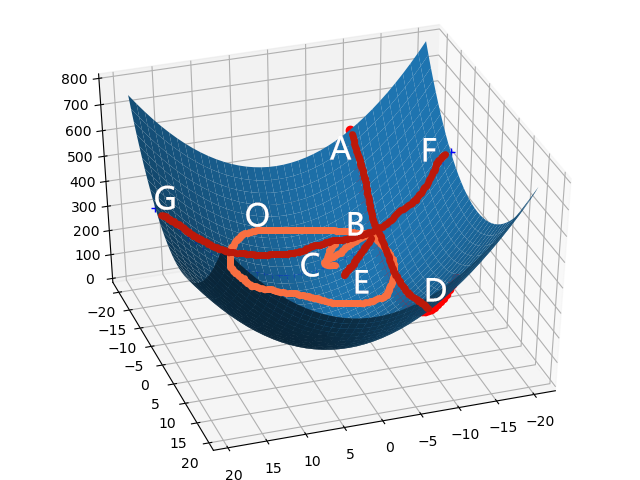
B点就是(-10,-10,200),O是过该点作的水平面,由于该函数为二元函数,所以梯度向量为x,y组成的二维向量,所以该向量必定在O平面中,具体就是(-20,-20),图中BC向量为与梯度方向相反的向量,是(20,20),沿着该方向走,即在曲面上BE走,就是该函数值减小最快的方向。
(2)u(x,y,z)=x**2+y**2+z**2
该函数为三元函数,实际上它是个体,可以想象成在原点吹气球,气球不断膨胀所包含的体,该函数的梯度向量为x,y,z所组成的三维向量,设点(x0,y0,z0)为该体的某一点,该点沿着(2x0,2y0,2z0)的方向,函数值将增加的最快,而该向量正好也是该点所在的球面的法向向量(方向朝外),如果沿着跟该方向垂直的方向走,函数值将不变,因为它还在该点所在的球面上,上述的几点也跟确实与我们的生活经验吻合。