一、小结
1.二叉树
定义与性质:
(1) 二叉树有五种基本形态;
(2) 在二叉树的 第 i 层上至多有 2^(i-l) 个结点(i>=1);
(3) 深度为 k 的 二叉树至多有 2^k -1 个结点 (k>=1);
(4) 叶子结点数 = 度为2结点数+1;
(5) 满二叉树是完全二叉树的一种;还有更常见的非完全二叉树;
二叉树的存储与遍历:
(1) 适合用顺序存储结构的二叉树种类较少,更多会使用链式存储结构,但无论如何,都要根据实际问题设计合适的 结点结构 和 存储结构;
(2) 遍历二叉树是二叉树最基本的操作,其他各种操作的基础;
(3) 基于二叉树的递归定义有 先序、中序、后序三种遍历算法;时间复杂度为O(n);
(4) 线索二叉树除了能得到左右孩子结点的信息,还能直接的到结点的前驱和后继信息。
2.树与森林
树的存储与遍历:
(1) 常见的存储结构有双亲表示法、孩子表示法、孩子兄弟法。可根据具体问题作出节省空间或节省时间上的改进;
(2) 森林或树与二叉树可进行相互转换;
(3) 森林有两种基于递归定义的遍历方法:先序和中序;
3.哈夫曼树
(1) 带权路径长度最小的二叉树称为哈夫曼树;权值越大的结点离根结点越近;
(2) 左分支标记为 0, 右分支标记为 1,则根结点到每个叶子结点路径上的 0、1序列即为相应字符的编码,如下图
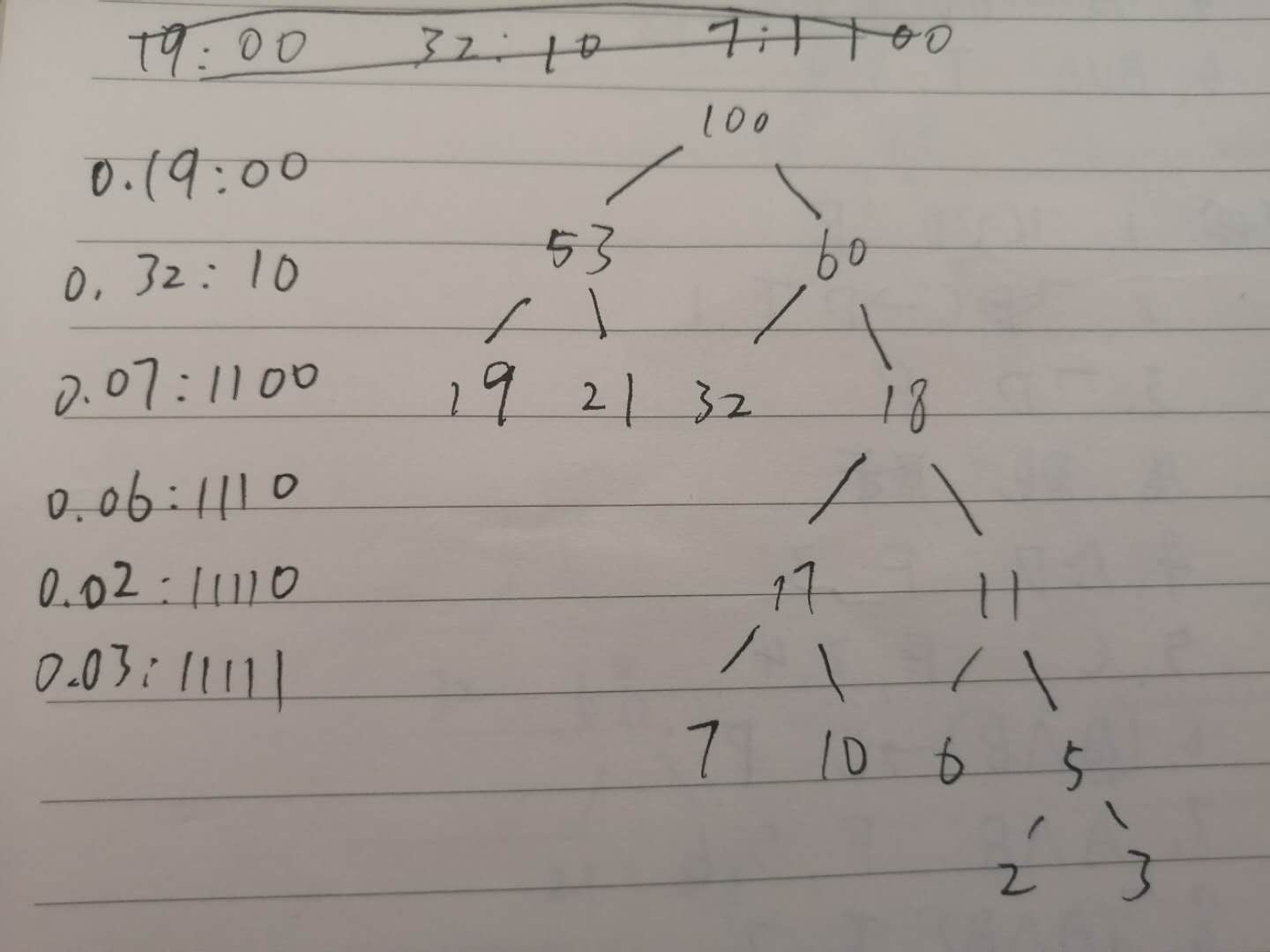
二、感想:
感觉比第四章简单了一丢丢(可能老师手下留情),因为把树的结点线性化后,基本操作还是基于线性表,只是在解决具体问题时,
设计怎样的结点、设计怎样的遍历方法能够适用于当前问题,是需要实操前多思考多比较的