本文是摘抄学习大神 计算机的潜意识 文章 https://www.cnblogs.com/subconscious/p/5058741.html
神经网络是一种模拟人脑的神经网络,期望能够实现类人的人工智能机器学习技术。
一、经典神经网络模型
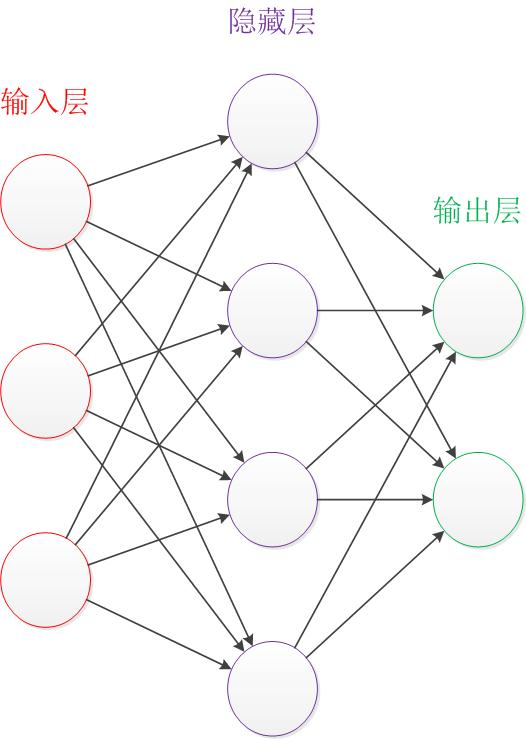
这个模型包含三个层次的神经网络,红色是输入层(3个输入单元),绿色是输出层(2个单元),紫色是隐藏层(4个单元)
神经网络模型知识点:
- 输入层和输出层的节点数一般是固定的,隐藏层可以自由设定
- 神经网络结构图的拓扑与箭头代表预测过程数据的流向,和训练的数据流有一定的区别
- 结构图的关键不是神经元(图中圆圈),而是连接线(图中圆圈的连接线),每个连接线对应一个不同的权重(值称为权值),权重是训练得到
二、神经元模型
神经元包含输入、输出和计算功能的模型,下图包含3个输入、1个输出、以及二个计算功能的模型
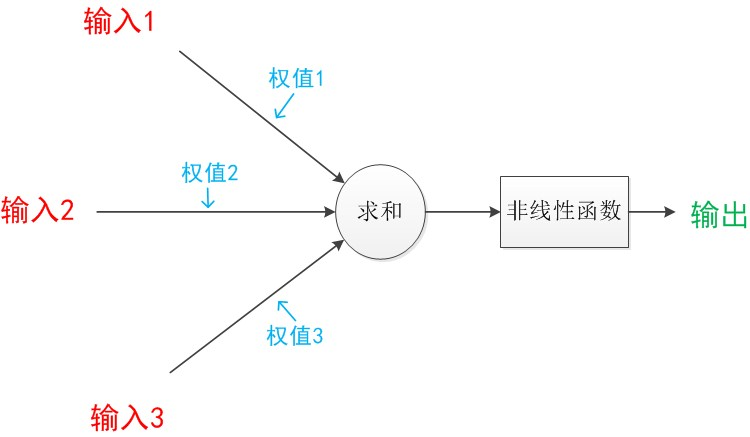
连接是神经元中最重要的东西,每个连接上都有一个权重。
神经网络算法就是让权重值调整到最佳,以到达模型预测的效果最好。
使用a表示输入特征变量,w来表示权重值,一个连接的有向箭头表示:a经过连接加权变成了aw

对于多特征变量的神经元模型,如下图,其中:z = g(a1w1+a2w2+a3w3)为输出计算公式
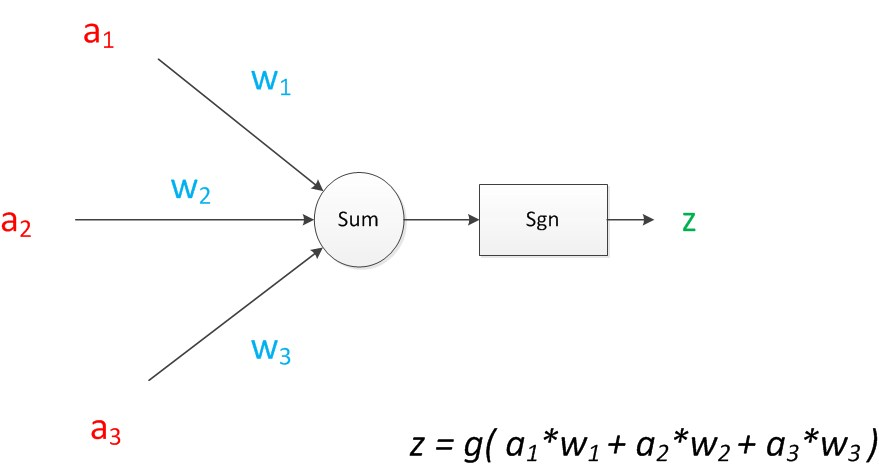
在MP模型里,函数g是sgn函数:当输入大于0时输出为1,小于0是输出为0
把sum函数和sgn函数合并,神经元可以看作一个计算和存储单元,计算是神经元对输入进行计算,存储是神经元会暂存计算结果,并传递到下一层。
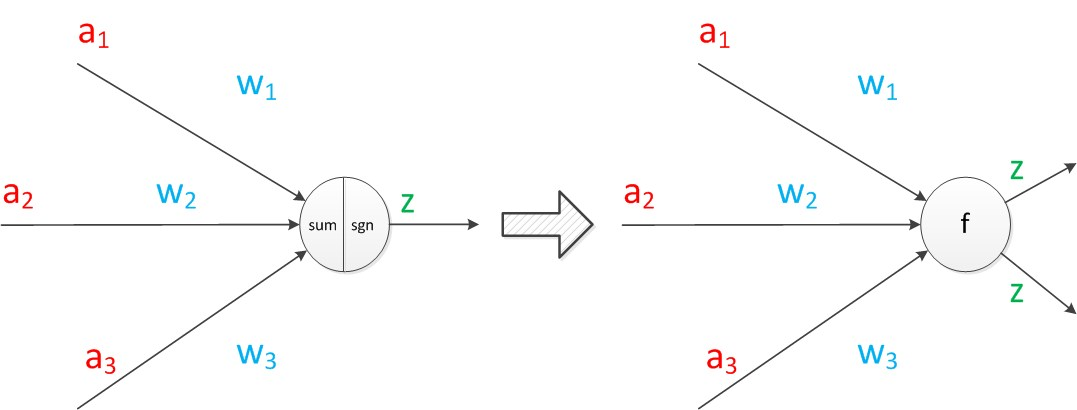
整个模型就是对函数:z = g(a1w1+a2w2+a3w3)结果的预测,通过已知的样本a1,a2,a3特征和对应的标签z1,z2,z3,得出最优的w1,w2,w3权重,最后预测出z标签值
三、单层神经网络
在MP模型的输入位置添加神经元节点,标志其为输入单元(负责传输数据,不计算),输出层的输出单元需要对前一层对输入进行计算。

有两个输出单元的模型,用wx,y来表达一个权值。下标中的x代表后一层神经元的序号,而y代表前一层神经元的序号(序号的顺序从上到下)。
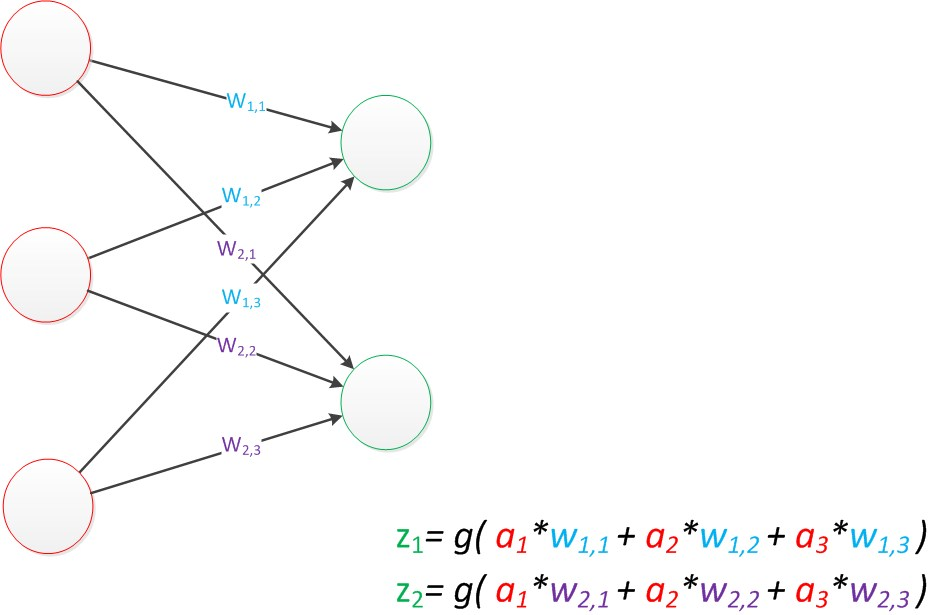
分析图上两个公式,可以向量化:
输入特征变量:a = [a1 a2 a3]T(T代表转置矩阵),预测值:z = [z1 z2]T,权重矩阵W(2X3矩阵)
输出公式向量化表示: z = g(Wa) (神经网络前一层计算后一层的矩阵运算)
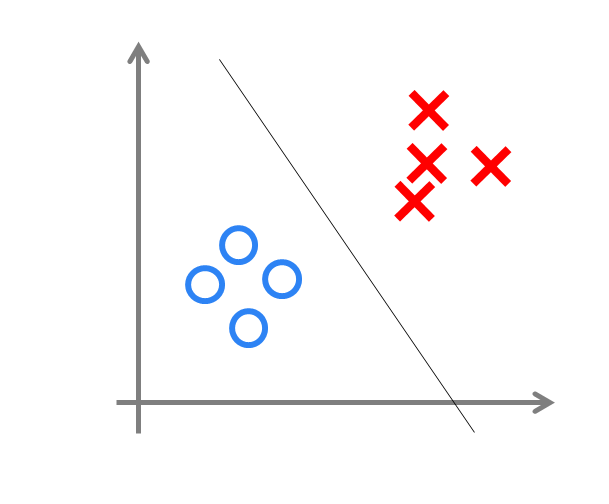
神经网络类似一个logistic回归,可以做分类任务。决策界限表示分类效果
四、两层神经网络模型
两层神经网络包含一个输入层、一个输出层和一个隐藏层,隐藏和输出层都是计算层。
ax(y)代表第y层的第x个节点。z1,z2变成了a1(2),a2(2)。下图给出了a1(2),a2(2)的计算公式


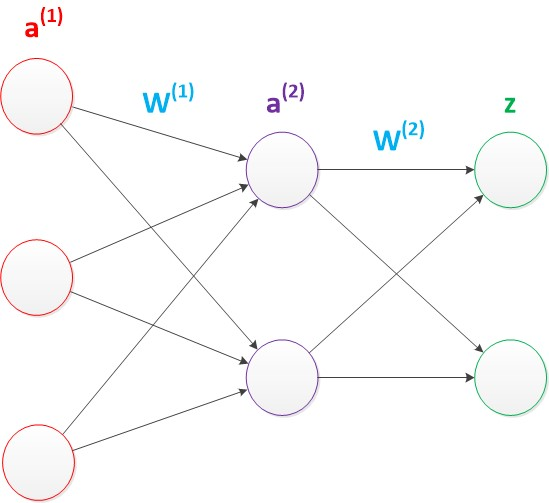
使用矩阵来进行向量化,a1,a2,z是网络传输的向量数据,W1和W2是网络的矩阵参数
a2 = g(W1a1)
z = g(W2a2)
由此可见,使用矩阵来向量化不会受到节点的数量影响,因此神经网络大量使用矩阵运算来描述。
偏置节点:它本质上是一个只函数存储功能,切存储值永远为1的单元,除了输出层外,神经网络的每个层都含有一个偏置单元,跟线性回归模型和逻辑(logistic)回归模型相同。
偏置单元与后一层的所有节点都有连接,设参数为向量b,称为偏置
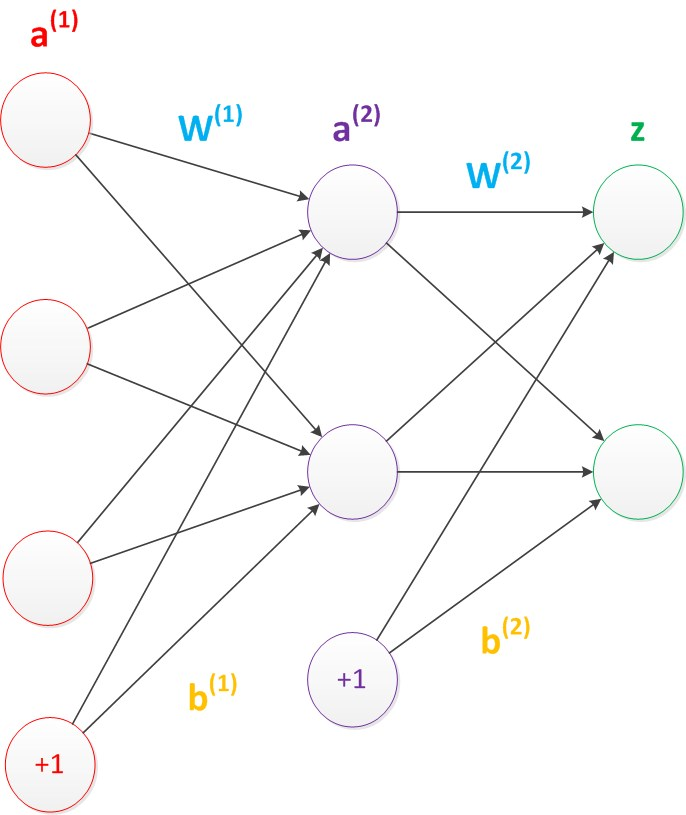
偏置节点没有输入,在考虑偏置后神经网络的矩阵运算:
a2 = g(W1a1 + b1)
z = g(W2a2 + b2)
g函数为sigmoid函数又称logistic函数、激活函数:g(x) = 1/(1+e-x),输入大于0时输出为1,小于0是输出为0。
理论证明,两层神经网络可以无限逼近任意连续函数
隐藏层的节点数设计
在设计一个神经网络是,输入层的节点数需要与特征的维度匹配,输出层的节点数也要与目标的维度匹配,而隐藏层的节点数,由设计者指定,但是节点数设置多少,却会影响模型的效果,如何决定这个自由层的节点数呢?目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值,通过切换这几个值来看整个模型的预测效果,选择效果最好的值作为最终选择。这种方法又叫做Grid Search(网格搜索)
了解了两层神经网络的结构以后,我们就可以看懂其它类似的结构图。例如EasyPR字符识别网络架构(下图)。
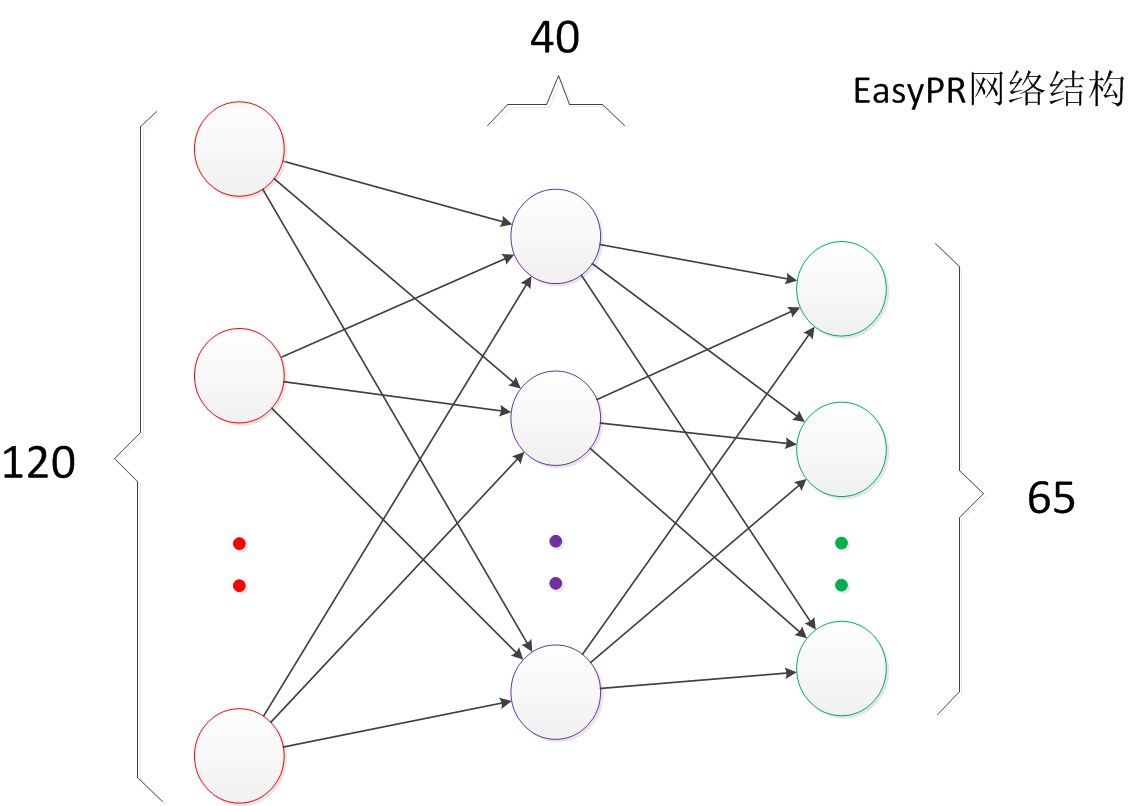
EasyPR使用了字符的图像去进行字符文字的识别。输入是120维的向量。输出是要预测的文字类别,共有65类。根据实验,我们测试了一些隐藏层数目,发现当值为40时,整个网络在测试集上的效果较好,因此选择网络的最终结构就是120,40,65。
前向传播:输入层--> 隐藏层--> 输出层
反向传播
参考:
1、《机器学习》(吴恩达)
2、计算机的潜意识:https://www.cnblogs.com/subconscious/p/5058741.html