1、k均值聚类模型
给定样本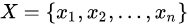 ,每个样本都是m为特征向量,模型目标是将n个样本分到k个不停的类或簇中,每个样本到其所属类的中心的距离最小,每个样本只能属于一个类。用C表示划分,他是一个多对一的函数,k均值聚类就是一个从样本到类的函数。
,每个样本都是m为特征向量,模型目标是将n个样本分到k个不停的类或簇中,每个样本到其所属类的中心的距离最小,每个样本只能属于一个类。用C表示划分,他是一个多对一的函数,k均值聚类就是一个从样本到类的函数。
2、k均值聚类策略
k均值聚类的策略是通过损失函数最小化选取最优的划分或函数 。
。
首先,计算样本之间的距离,这里选欧氏距离平方。
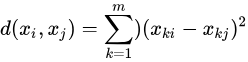
然后定义样本与其所属类的中心之间的距离的总和为损失函数
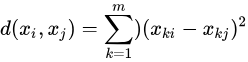
其中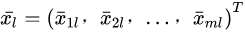 为第l个类的均值或中心
为第l个类的均值或中心
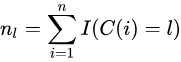
,是指示函数,取值1或0.
k均值聚类就是求解最优化问题:

3、k均值聚类算法
k均值聚类的算法是一个迭代过程,
首先:
对于给定中心值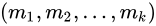 ,求划分C,是目标函数极小化:
,求划分C,是目标函数极小化:
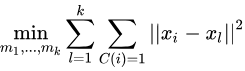
即,类中心确定的情况下,将样本分到一个类中,使样本和其所属类的中心之间的距离总和最小。
然后:
对于给定的划分C,再求各个类的中心,是目标函数极小化。
即,划分C确定的情况下,使样本和其所属类的中心之间的距离总和最小。求解结果,对于每个包含nl个样本的类Gi,更新其均值ml:
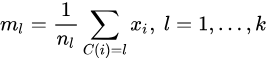
重复以上两个步骤,知道分化不在改变。
from myUtil import *
def kMeans(dataSet, k):
m = shape(dataSet)[0] # 返回矩阵的行数
# 本算法核心数据结构:行数与数据集相同
# 列1:数据集对应的聚类中心,列2:数据集行向量到聚类中心的距离
ClustDist = mat(zeros((m, 2)))
# 随机生成一个数据集的聚类中心:本例为4*2的矩阵
# 确保该聚类中心位于min(dataSet[:,j]),max(dataSet[:,j])之间
clustercents = randCenters(dataSet, k) # 随机生成聚类中心
flag = True # 初始化标志位,迭代开始
counter = [] # 计数器
# 循环迭代直至终止条件为False
# 算法停止的条件:dataSet的所有向量都能找到某个聚类中心,到此中心的距离均小于其他k-1个中心的距离
while flag:
flag = False # 预置标志位为False
# ---- 1. 构建ClustDist:遍历DataSet数据集,计算DataSet每行与聚类的最小欧式距离 ----#
# 将此结果赋值ClustDist=[minIndex,minDist]
for i in xrange(m):
# 遍历k个聚类中心,获取最短距离
distlist = [distEclud(clustercents[j, :], dataSet[i, :]) for j in range(k)]
minDist = min(distlist)
minIndex = distlist.index(minDist)
if ClustDist[i, 0] != minIndex: # 找到了一个新聚类中心
flag = True # 重置标志位为True,继续迭代
# 将minIndex和minDist**2赋予ClustDist第i行
# 含义是数据集i行对应的聚类中心为minIndex,最短距离为minDist
ClustDist[i, :] = minIndex, minDist
# ---- 2.如果执行到此处,说明还有需要更新clustercents值: 循环变量为cent(0~k-1)----#
# 1.用聚类中心cent切分为ClustDist,返回dataSet的行索引
# 并以此从dataSet中提取对应的行向量构成新的ptsInClust
# 计算分隔后ptsInClust各列的均值,以此更新聚类中心clustercents的各项值
for cent in xrange(k):
# 从ClustDist的第一列中筛选出等于cent值的行下标
dInx = nonzero(ClustDist[:, 0].A == cent)[0]
# 从dataSet中提取行下标==dInx构成一个新数据集
ptsInClust = dataSet[dInx]
# 计算ptsInClust各列的均值: mean(ptsInClust, axis=0):axis=0 按列计算
clustercents[cent, :] = mean(ptsInClust, axis=0)
return clustercents, ClustDist
参考:
https://jakevdp.github.io/PythonDataScienceHandbook
https://www.cnblogs.com/eczhou/p/7860424.html
统计学习方法14.3
