几种非线性激活函数介绍

1. 几种非线性激励函数(Activation Function)

神经网络中，正向计算时，激励函数对输入数据进行调整，反向梯度损失。梯度消失需要很多方式去进行规避。

1.1 Sigmoid函数

表达式为： 

 

y(x)=sigmoid(x)=11+e−x,y(x)in(0,1)y(x)=sigmoid(x)=11+e−x,y(x)in(0,1)

 

y(x)′=y(x)(1−y(x)),y′in(−∞,14]y(x)′=y(x)(1−y(x)),y′in(−∞,14]

该函数将输入映射到(0,1)（能否取到0和1，取决于计算机的精度），由导数可看出， 最大值为0.25，也即在反向计算时，梯度损失非常明显，至少减少75%，

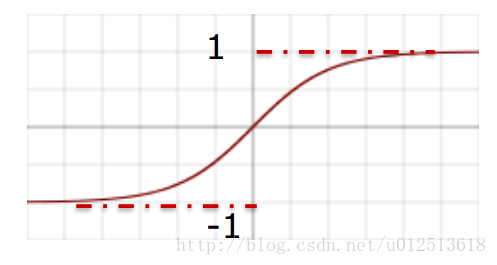
1.2 Tanh函数

表达式为： 

 

f(x)=tanh(x)=21+e−2x−1,f(x)in(−1,1)f′(x)=1−f(x)2,f′(x)in(0,1)f(x)=tanh⁡(x)=21+e−2x−1,f(x)in(−1,1)f′(x)=1−f(x)2,f′(x)in(0,1)

该函数将输入映射到(-1,1)（能否取到-1和1，取决于计算机的精度），由导数可看出，在反向计算时，梯度也会有所损失。倘若网络深度非常深，梯度消失(gradient vanishing)。 

1.3 ReLU ( Rectified Linear Unit)函数

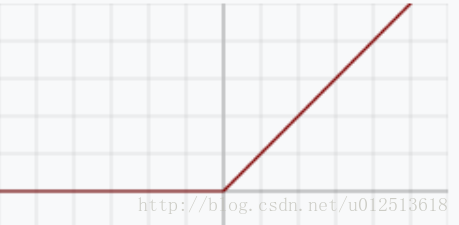
表达式为： 

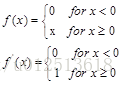
该函数将输入分两个段进行映射，当输入值小于0时，则将原值映射为0，若输入值大于0则按照原值传递，即，正向计算的时候，会损失特征大量，由导数可看出，在反向计算时，梯度没有损失。 

(1) ReLU的优缺点

1. 1) 优点1：

Krizhevsky et al. 发现使用 ReLU 得到的SGD的收敛速度会比 sigmoid/tanh 快很多。有人说这是因为它是linear，而且梯度不会饱和

• 2) 优点2：

相比于 sigmoid/tanh需要计算指数等，计算复杂度高，ReLU 只需要一个阈值就可以得到激活值。

• 3) 缺点1：

  ReLU在训练的时候很”脆弱”，一不小心有可能导致神经元”坏死”。 
  举个例子：由于ReLU在x<0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，也就是ReLU神经元坏死了，不再对任何数据有所响应。实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都坏死了。 当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。

(2) ReLU正向截断负值，损失大量特征，为什么依然用它？

答：特征足够多，反向梯度无损失！

1.4 Leaky ReLU(Leaky Rectified Linear Unit)

表达式如下： 

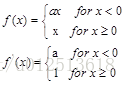
Leaky ReLU. Leaky ReLUs 就是用来解决ReLU坏死的问题的。和ReLU不同，当x<0时，它的值不再是0，而是一个较小斜率(如0.01等)的函数。也就是说f(x)=1(x<0)(ax)+1(x>=0)(x),其中a是一个很小的常数。这样，既修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。关于Leaky ReLU 的效果，众说纷纭，没有清晰的定论。有些人做了实验发现 Leaky ReLU 表现的很好;有些实验则证明并不是这样。 
-PReLU. 对于 Leaky ReLU 中的a，通常都是通过先验知识人工赋值的，比如说0.01