堆与堆排序 红黑树

参考：http://blog.csdn.net/morewindows/article/details/6709644

　　数组的堆化

　　把一个无序数组，原地变成堆的结构。

　　

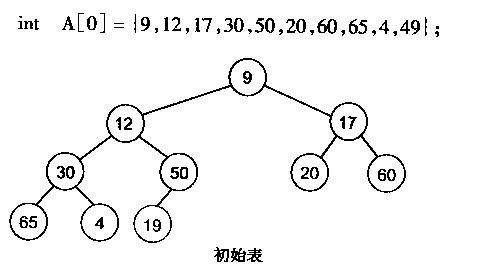
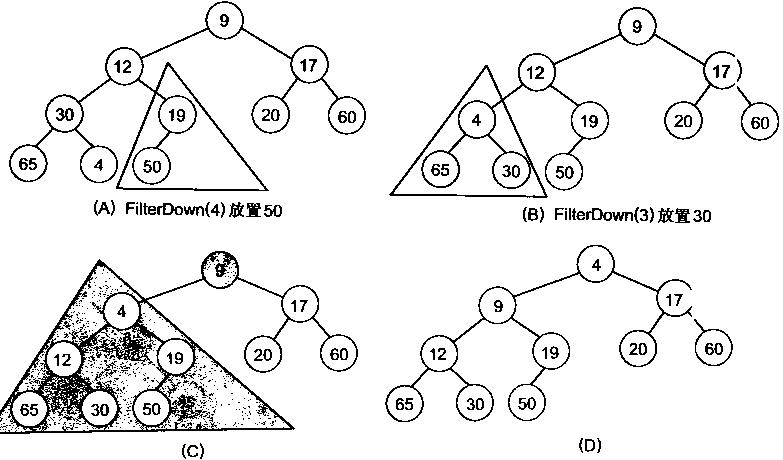
　　上图是堆化成最小堆的结构。

　　可以看到，它是按照由小树 -> 到大树的逐步堆化。这样做是为了避免使用第二个数组。

　　假如是大树 到 小树 的堆化，在大树的堆化时，它并不能保证父节点的一次堆化能取到最小(大)的元素。而小树到大树的结构，可以保证小树的根节点肯定是小树的最小元素，从而保证大树只需判断左儿子和右儿子就能取到最小值。

package algorithm;
//堆排序
public class HeapSort {
    
    public static void main(String[] args) {
        int[] arr = {6,4,2,8,1,9};
        heapSort(arr);
    }
    public static void heapSort(int[] arr){
        for (int i = (arr.length>>>1)-1; i >= 0; i--) { //从小树到大树的逐步堆调整
            heapAdjust(arr,i,arr.length);
        }
        for (int i = arr.length-1; i > 0; i--) { //逐步找到最大的元素，放在最后，减少堆的长度(i)
            int temp = arr[0]; //交换最大和最后个
            arr[0]=arr[i];
            arr[i] = temp;
            heapAdjust(arr,0,i); //调整堆结构
        }
        for (int i : arr) {
            System.out.println(i);
        }
    }
    
    public static void heapAdjust(int[] arr, int i,int n){
        int child = 0;    //儿子为 2*i+1 和 2*i+2
        for (; (child=(i<<1)+1) < n; i=child) { //堆调整,父亲到儿子的逐步迭代
            if (child<n-1 && arr[child+1]>arr[child]) //右儿子较大，注意检查右儿子是否越界
                child++;
            if (arr[child]>arr[i]) { //交换儿子和父亲
                int temp = arr[i];
                arr[i] = arr[child];
                arr[child] = temp;
            }else     //不用交换 迭代结束
                break;
        }
    }
}