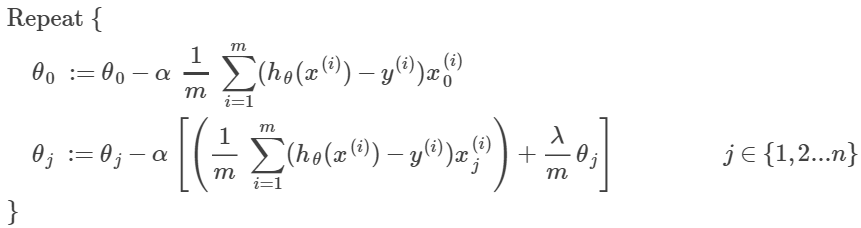逻辑回归(logistic regression)
1.用来解决归类问题(只是由于历史上的原因取了回归的名字)
2.二分归类(binary classification)
- 定义:对于输入,输出值不连续,而是两个离散的值,eg:{0,1}
- 方法:利用线性回归,将大于0.5的输出预测值设为1,小于0.5的输出预测值设为0.(目前不可行,因为归类问题不是线性函数,所以引入S型函数(Sigmoid Function)/逻辑函数(logistic function))
- Sigmoid Function / logistic function
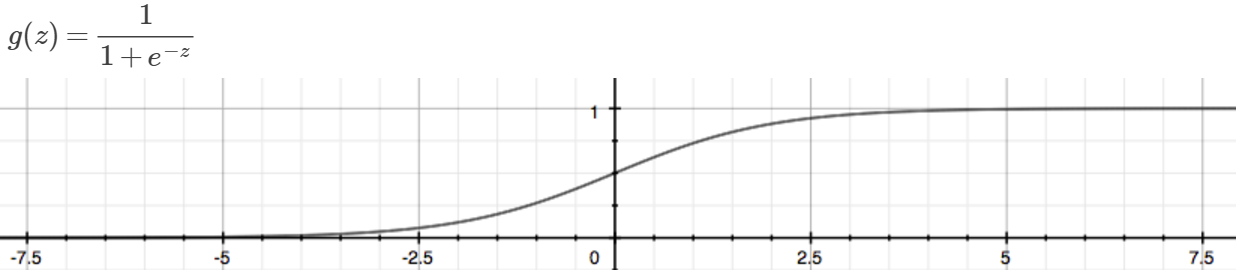
z>=0时g>=0.5,z<0时g<0.5; z-> -∞,g->0; z-> +∞,g->1
![]() ,
, ![]() ,
, ![]()
h(x)为输出值为1的概率:
![]()
- 为了得到离散的归类,假设:
![]() ,所以有:
,所以有:
![]()
- 决策边界(decision boundry):将y=0和y=1的区域分开的那条线(对应上面来说就是θ'x=0那个方程)
- 代价方程(cost function):

合并上面两个式子:

再向量化表示:
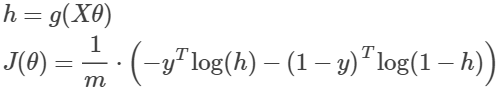
画图是:
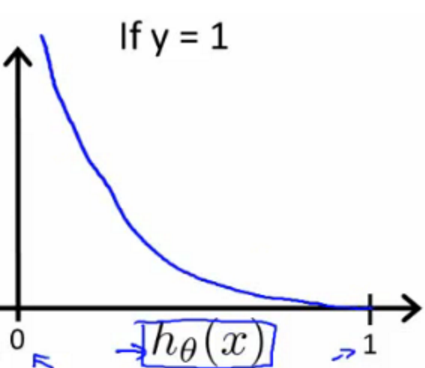
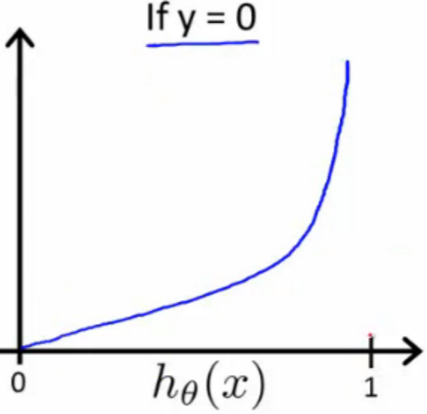
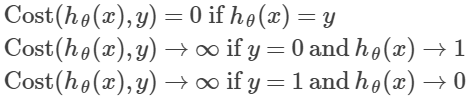
- 梯度下降(gradient decent):
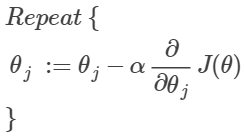
求偏导可得:(和之前线性回归的结果一样)
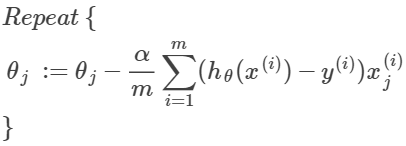
向量化表示为:
![]()
- 比梯度下降更优的求θ的方法:
Conjugate gradient, BFGS, L-BFGS
用octave内部的函数库来调用这些方法,步骤:
1.写出代价函数和它的偏导:
function [jVal, gradient] = costFunction(theta) jVal = [...code to compute J(theta)...]; gradient = [...code to compute derivative of J(theta)...]; end
2.调用fminunc函数,optimset是传给该函数的参数
options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
3.多类归类(multiclass classification):
- 结果为多个类别,y={0,1,....n}
- 这种情况下,可以将问题分为n+1个二分归类问题,选择一个类,将其他所有类看成一个类,利用二分归类,求出每个h(x),再求最大值
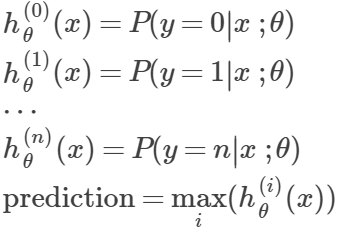
正规化(regularization)
1.正规化用来解决过拟合问题(overfitting),适用于线性回归和逻辑回归问题。
延伸:
- h函数太简单:欠拟合,高偏差(underfitting,high bias)
- h函数太复杂:过拟合,高方差(overfitting,high variance)
- 解决过拟合方法有:减少参数(人工进行参数选择或者用特定的参数选择算法)、正规化
2.正规化后的代价函数:
![]() (λ是正规化参数)
(λ是正规化参数)
演示:https://www.desmos.com/calculator/1hexc8ntqp
eg:
h(x)= ![]()
如果想要减少theta3,theta4参数的影响,代价函数可以写成如下形式:
![]()
后面的两项参数乘以很大的数,这样为了得到代价的最小值,后两个参数就得很小,趋近于0,这样h函数中的那两个参数就
会很小,相当于消去了参数,所以函数就会变得平缓了,从而不会过拟合
3.正规化线性回归:
- 梯度下降变为:(多了λ项)
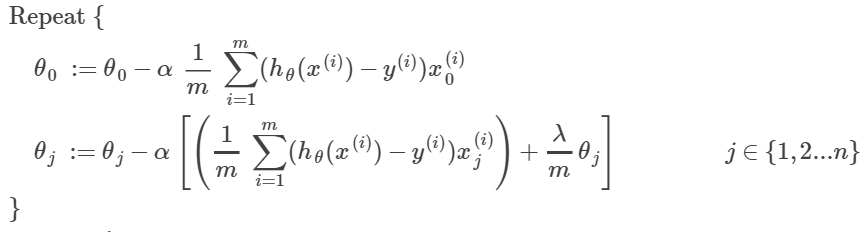
移项也可以写成:
![]()
可以看出,和没有正规化相比,只是每次迭代时,theta都变为原来的(1-α*λ/m)<1倍
- 不迭代的nomal equation为:
 ( L=(n+1)*(n+1) )
( L=(n+1)*(n+1) )
4.正规化逻辑回归:
- 代价函数为:(多了λ项)
![]() (注意没有第0项)
(注意没有第0项)
- 梯度下降:(和线性回归正规化的一样)