题目
Description
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的 1 表示墙壁,0 表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
Input
一个5 × 5的二维数组,表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径,格式如样例所示。
Sample Input
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
解题思路
这题是迷宫求最短路径问题,由于迷宫的边权都为 1, 所以优先使用宽度优先搜索 BFS来做
当BFS找到终点时,说明找到了一条最短路径,所以要有一个记录当前路径的方法
*** 判断遍历到终点的方法 ***
if ( tx == 4 && ty == 4 ) return tt - 1;
这里的做法是开一个struct数组来当队列,里面包含了当前遍历到的点x, y与当前点的父节点位置(由父节点扩展到点x,y)
找到终点时,我们从终点开始看,找到它父节点在队列中的位置,记录它信息(x, y),再把这个父节点当成起始点,再次回溯它的父节点...
将父节点内存储的坐标逐一压入堆栈中,当回溯的父节点位置为-1时,停止回溯,开始将堆栈中的内容全部弹出打印。
注释代码
#include <iostream>
#include <stack>
#include <cstdio>
using namespace std;
const int N = 30;
typedef pair<int, int> PII;
/* 堆栈 stack 的元素为 pair ,以 .first 和 .second 的方式访问 pair 内的两个元素 */
stack<PII> stck;
struct stu {
int x;
int y;
int p; /* p 即为 当前点的父节点在队列 q 中的下标 */
} q[N]; /* q 即为 队列, 使用数组来模拟队列 */
/* 存放地图数据 */
int a[10][10];
/* 表示 x, y 这个点是否进入过队列,每个点最多只进入队列一次(优化) */
bool st[N][N];
/* 下一个点的方向 */
int ne[2][4] = { {0, -1, 0, 1 }, {1, 0, -1, 0} };
/* bfs 返回终点在队列中的位置 */
int bfs ( void )
{
int hh = 0, tt = 0; // 队头hh 队尾tt
q[tt++] = { 0, 0, -1 }; // 添加队头元素,父节点设置为-1,表示这是队头
st[0][0] = true; // (0, 0)点已添加进队列
while ( tt > hh ) // 队列不为空则循环
{
struct stu t = q[hh++]; // 取队头元素
/* 枚举四个方向 */
for ( int i = 0; i < 4; i++ )
{
int tx = t.x + ne[0][i];
int ty = t.y + ne[1][i];
/*
三大判断条件
1、tx,ty在边界内
2、当前点的值为 0
3、当前点未被加入过队列
*/
if ( tx >= 0 && ty >= 0 && tx <= 4 && ty <= 4 && !st[tx][ty] && a[tx][ty] == 0 )
{
st[tx][ty] = true;
q[tt++] = {tx, ty, hh - 1}; // 当前队首 - 1即为它的父节点
}
if ( tx == 4 && ty == 4 ) return tt - 1;
}
}
}
int main ( void )
{
/* 将输入数据存入地图中 */
for ( int i = 0; i < 5; i++ )
for ( int j = 0; j < 5; j++ )
cin >> a[i][j];
int t = bfs(); // 接收BFS的返回值,此时 t 代表终点在队列 q 中位置
/*
i = t
只要 i != -1,意思就是没有遍历到头节点 就一直循环,
每次循环后更新 i = q[i].p 意思是让 i 变为当前 i 所表示点的父节点的位置
每次循环将当前的坐标压入堆栈
*/
for ( int i = t; i != -1; i = q[i].p )
stck.push ( {q[i].x, q[i].y} );
/*
只要堆栈不为空,就弹出栈顶元素并输出
*/
while ( !stck.empty() )
{
PII i = stck.top();
stck.pop();
printf ( "(%d, %d)
", i.first, i.second );
}
return 0;
}
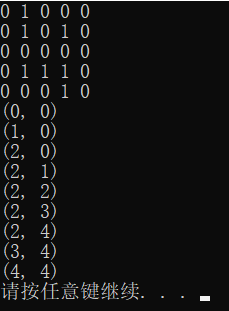
输入 / 输出:
如果有写的不好的地方,或者有哪里还没有理解的地方,请积极留言