[题解] Codeforces Round #694 (Div. 2) B题 解题报告

B题

给定一个原始数组(a)，长度为(n)，再给定一个整数(x)。

可以创建一个队列(q)，将原始数组放到该队列，遍历队列。

如果当前元素 (q[head]) 能整除以(x)，则将(x)个 (q[head] / x) 的结果放入到队列尾，当q[head]不能整除以(x)，则停止操作，计算当前队列的元素总和。

所求输出即为当前队列的元素总和。

简单模拟了一下数据可以发现，

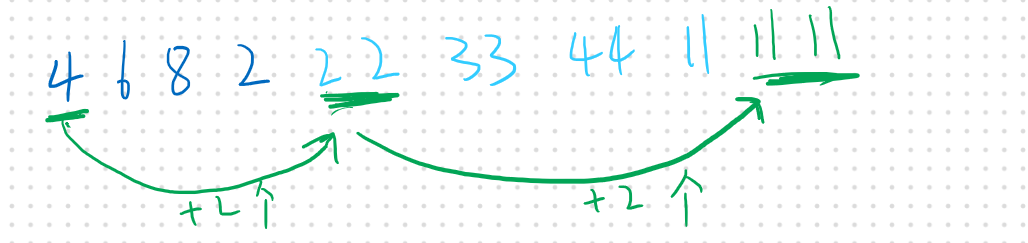
第一组数据可以派生出第二组数据，第二组数据可以派生出第三组数据

而派生后的总数量也是与组数和(x)有一定关系的，如：

第一组的一个数据派生到第二组，个数变为了x个

再次派生到第三组，数量变到了(x * x)个
(...)
即第n组的数量为为 (x^{(n-1)})个

所以在往队列添加元素的时候只需要添加一个数据，同时将答案自加(x^{(i-1)}*head[i])即可,大大降低了对空间的需求

代码如下：

#include <iostream>
#include <cmath>
#include <queue>

using namespace std;

typedef long long ll;
typedef pair<int, int> PII;  // 当前的数，第几组数据

const int N = 1e5 + 10;

ll solve ( void )
{
	bool st = false;
	ll sum = 0;
	queue<PII> q;

	int n, x;
	cin >> n >> x;

	for ( int i = 0; i < n; i++ )
	{
		int u;
		scanf ( "%d", &u );
		q.push ( {u, 0} );
	}

	while ( !q.empty() )
	{
		PII t = q.front();
		int a = t.first, r = t.second;
		
		q.pop();
		sum += a * pow ( x, r );

//              如果进入了if语句则说明达到终止条件，无需向队列尾添加元素了，只需要计算出队列中剩余项的总和即可
		if ( st || a % x != 0 )
		{
			st = true;
			continue;
		}

		q.push ( {a / x, r + 1} );
	}

	return sum;
}

int main ( void )
{
	int T;
	cin >> T;

	while ( T-- ) cout << solve() << endl;

	return 0;
}