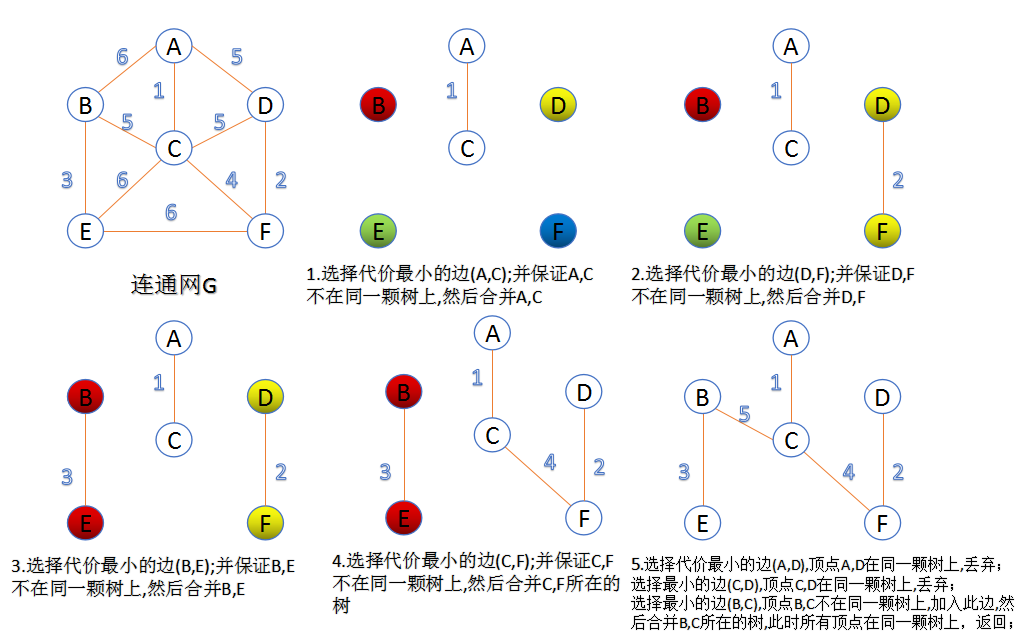
Kruskal算法&Prim算法

最小生成树是什么？

Kruskal算法

图文转载自a2392008643的博客

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；

2. 把图中的n个顶点看成独立的n棵树组成的森林；

3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。

4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

代码:(题目:LOJ#123最小生成树)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll f[200005],n,m;
void init(ll m) {for(ll i=1;i<=m;i++) f[i]=i;}
ll getf(ll x) {return f[x]==x?x:f[x]=getf(f[x]);}
bool merge(ll t1,ll t2) {return getf(t1)==getf(t2)?false:(f[getf(t2)]=getf(t1),true);}
struct node{ll x,y,co;}a[500005];
bool cmp(node a,node b) {return a.co<b.co;}
int main()
{
	scanf("%lld %lld",&n,&m);
	for(ll i=1;i<=m;i++) scanf("%lld %lld %lld",&a[i].x,&a[i].y,&a[i].co);
	sort(a+1,a+m+1,cmp);
	init(n);
	ll num=0,sum=0;
	for(ll i=1;i<=m;i++)
	{
		if(merge(a[i].x,a[i].y)) ++num,sum+=a[i].co;
		if(num==n-1) break;
	}
	printf("%lld",sum);
	return 0;
}

---

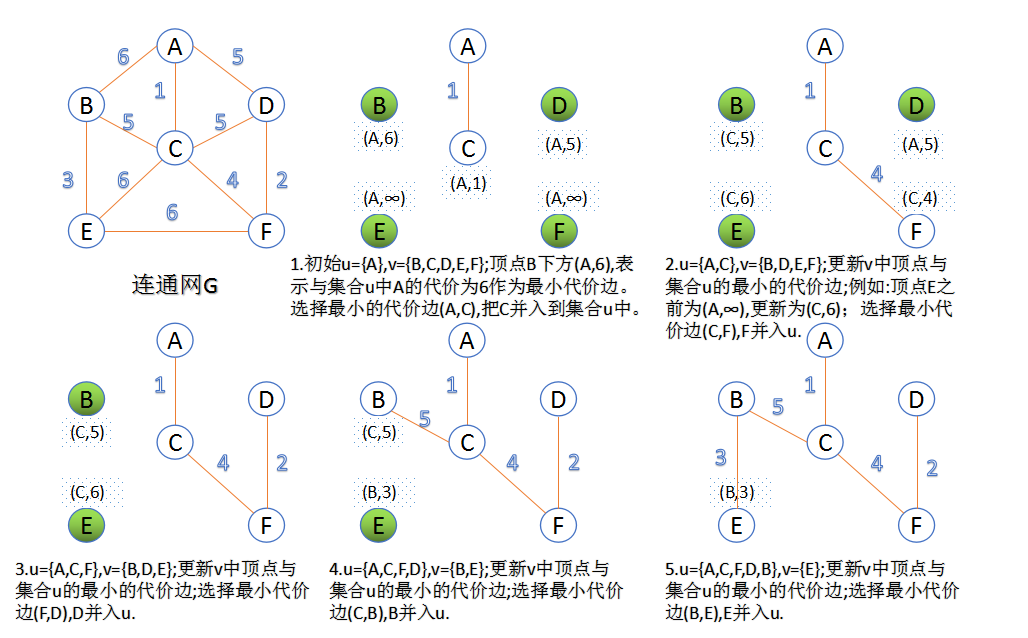
Prim算法

图文转载自a2392008643的博客

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为V；初始令集合u={s},v=V−u={s},v=V−u;

在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。

重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

代码:(不加优化)

#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL n,m,a[5005][5005],vst[5005],dis[5005],ans=0;
void prim(int x)
{
    LL i,j,k,minn;
    memset(vst,0,sizeof(vst));
    memset(dis,0x7f7f7f7f,sizeof(dis));
    dis[x]=0;
    ans=0;
    for(i=1;i<=n;i++)
    {
        minn=0x7f7f7f7f;
        for(j=1;j<=n;j++)
        {
            if(vst[j]==0&&minn>dis[j])
            {
                minn=dis[j];
                k=j;
            }   
        }
        vst[k]=1;
        ans+=dis[k];
        for(j=1;j<=n;j++)
        {
            if(vst[j]==0&&dis[j]>a[k][j]) dis[j]=a[k][j];
        }
    }
}
int main()
{
    LL i,j,k,s=0,flag=0,x,y,z;
    cin>>n>>m;
    memset(a,0x7f7f7f7f,sizeof(a));
    for(i=1;i<=m;i++)
    {
        cin>>x>>y>>z;
        a[x][y]=a[y][x]=z;
    }
    prim(1);
    cout<<ans;
    return 0;
}

代码:(邻接表+堆优化)

#include<bits/stdc++.h> 
using namespace std;
#define ll long long 
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que;
int head[200010],nxt[1000010],edge[1000010],ver[1000010],tot=0,dis[200010];
bool book[200010];
int n,m,cnt;
ll ans=0;
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	nxt[tot]=head[x];
	head[x]=tot;
}
int main()
{
	scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        add(a,b,c),add(b,a,c);
    }
    que.push(make_pair(0,1));
    while(!que.empty()&&cnt<=n)
    {	
        int u=que.top().second,v=que.top().first;
        que.pop();
        if(book[u]) continue;
        book[u]=true;
		cnt++;ans+=v;
        for(int i=head[u];i;i=nxt[i])
        	if(!book[ver[i]])
    			que.push(make_pair(edge[i],ver[i]));
    }
    printf("%lld",ans);
    return 0;
}

---

对比

	不加优化的Prim	堆优化的Prim	Kruskal
时间复杂度	(mathcal O(n^2))	(mathcal O(mlog n))	(mathcal O(mlog m))
适用情况	稠密图	稠密图	稀疏图