Spring_day02
上节内容回顾
|
1 spring的概念 (1)核心:ioc和aop (2)spring一站式框架 2 spring的bean管理(xml) (1)bean实例化 (2)注入属性 (3)注入对象属性 3 ioc和di (1)ioc:控制反转,把对象创建交给spring管理 (2)di:依赖注入,创建对象过程中,向属性设置值 4 在服务器启动时候加载配置文件,创建对象 (1)ServletContext对象 (2)监听器 |
今天内容介绍
|
1 spring的bean管理(注解) (1)使用注解创建对象 - 四个注解 (2)使用注解注入属性 - Autowired - Resource (3)xml和注解方式混合使用 - 创建对象使用配置文件,注入属性使用注解 2 AOP (1)aop概述 (2)aop底层原理 (3)aop操作相关术语 - 切入点 - 增强 - 切面 3 spring的aop操作(基于aspectj的xml方式) 4 log4j介绍 5 spring整合web项目演示 |
Spring的bean管理(注解)
注解介绍
|
1 注解:代码里面特殊标记,使用注解可以完成功能 2 注解写法 @注解名称(属性名称=属性值) 3 注解使用在类上面,方法上面 和 属性上面 |
Spring注解开发准备
|
1 导入jar包 (1)导入基本的jar包
(2)导入aop的jar包
2 创建类,创建方法
3 创建spring配置文件,引入约束 (1)第一天做ioc基本功能,引入约束beans (2)做spring的ioc注解开发,引入新的约束
从后往前找找到context
4 开启注解扫描
|
注解创建对象
|
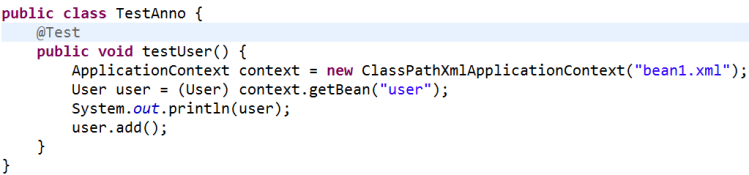
1 在创建对象的类上面使用注解实现
控制台输出: User的地址值 add............ 2 创建对象有四个注解
(1)@Component (2)@Controller (3)@Service (4)@Repository 目前这四个注解功能是一样的,都创建对象 3 创建对象单实例还是多实例
|
注解注入属性
|
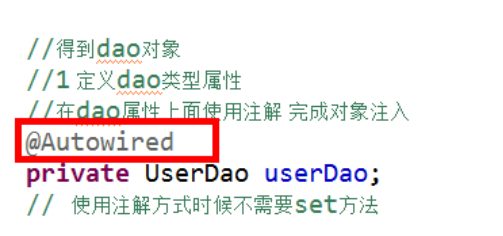
1 创建service类,创建dao类,在service得到dao对象 注入属性第一个注解 @Autowired (1)创建dao和service对象
(2)在service类里面定义dao类型属性
自动注入:根据UserDao类名称找到类对应的对象,注入进来 注入属性第二个注解 @Resource
在UserService类add()方法中就可以调用userDao类中的方法了
控制台: service....... dao...... |
配置文件和注解混合使用
|
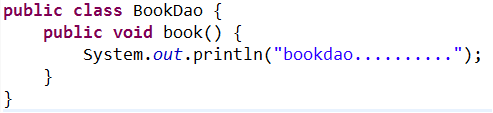
1 创建对象操作使用配置文件方式实现
2 注入属性的操作使用注解方式实现
控制台: service.......... bookdao....... ordersdao....... |