1 #include <iostream> 2 3 using namespace std; 4 #define LL long long 5 6 LL get_pow(LL x, LL n)//快速幂 7 { 8 LL ans = 1; 9 while(n) 10 { 11 if(n&1) 12 { 13 ans = x*ans; 14 } 15 x = x*x; 16 n>>=1; 17 } 18 return ans; 19 } 20 int main() 21 { 22 LL a, b; 23 while(cin >> a >> b){ 24 cout << get_pow(a, b) << endl; 25 } 26 return 0; 27 }
& 和 >>
& 运算通常用于二进制取位操作,例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶,x&1==1为奇。
>> 运算比较单纯, 二进制去掉最后一位

1 LL get_pow(LL x, LL n)快速幂 2 { 3 LL ans = 1; 4 while(n) 5 { 6 if(n&1)//判断是否为奇数 相当于 n % 2 7 { 8 ans = x*ans; 9 } 10 x = x*x; 11 n>>=1;//相当于 n /= 2 12 } 13 return ans; 14 }
递归
1 public static long pow(long x, int n) { 2 if(n == 0) 3 return 1; 4 else if((n&1) == 0) //偶数 5 return pow(x * x, n / 2); 6 else return pow(x * x, n / 2) * x; // 奇数 7 8 }
首先,快速幂的目的就是做到快速求幂,假设我们要求a^b,按照朴素算法就是把a连乘b次,这样一来时间复杂度是O(b)也即是O(n)级别,快速幂能做到O(logn),快了好多好多。它的原理如下:
把b转换成二进制数。 该二进制数第i位的权为

例如:
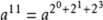
11 的二进制是 1011
11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1
因此,我们将a¹¹转化为算

 View Code
View Code

看出来快的多了吧原来算11次,现在算三次,但是这三项貌似不好求的样子....不急,下面会有详细解释。
以b==11为例,b=>1011,二进制从右向左算,但乘出来的顺序是 a^(2^0)*a^(2^1)*a^(2^3),是从左向右的。
我们不断的让 x*=x 目的即是累乘,以便随时对ans做出贡献。
其中要理解 x*=x 这一步,看 x *x = x^2 ,下一步再乘,就是x^2 * x^2 == x^4,然后同理
x^4 * x^4 == x^8
x--> x^2--> x^4--> x^8 --> x^16--> x^32.......指数正是 2^i ,
再看上 面的例子,
a¹¹= a^(2^0)*a^(2^1)*a^(2^3),
这三项解决了
快速幂取模
利用公式a*b%c=((a%c)*b)%c

1 ll get_pow(ll x, ll n){ 2 ll ans = 1; 3 while(n){ 4 if(n&1){ 5 // ans = x*ans%1000; 6 ans = (ans%1000*x)%1000; 7 } 8 x = (x%1000*x)%1000; 9 n >>= 1; 10 } 11 return ans%1000; 12 }
