简述:
二叉树是十分重要的数据结构,主要用来存放数据,并且方便查找等操作,在很多地方有广泛的应用。
二叉树有很多种类,比如线索二叉树,二叉排序树,平衡二叉树等,本文写的是最基础最简单的二叉树。
思路:
二叉树的建立采用的是递归的思想:给定一个指向根节点的指针,然后递归调用ceate()函数,自动生成一个二叉树。就像是在地上挖了个坑(根节点),然后他会拿着铲子(create函数)按照一定的规则自动挖一个很大的洞穴(二叉树)出来。当然挖坑前需要先定义每个洞长什么样(定义节点结构)。
二叉树的遍历采用的也是递归的思想:如果节点有数据,则按照遍历规则打印根节点和孩子节点,没有数据则返回直到所有数据都遍历完,递归结束。
不废话,上代码:
#include<iostream> using namespace std; //定义节点 typedef struct node { struct node *lchild; struct node *rchild; char data; }BiTreeNode, *BiTree; //*BiTree的意思是给 struct node*起了个别名,叫BiTree,故BiTree为指向节点的指针。 //按照前序顺序建立二叉树 void createBiTree(BiTree &T) //&的意思是传进来节点指针的引用,括号内等价于 BiTreeNode* &T,目的是让传递进来的指针发生改变 { char c; cin >> c; if('#' == c) //当遇到#时,令树的根节点为NULL,从而结束该分支的递归 T = NULL; else { T = new BiTreeNode; T->data=c; createBiTree(T->lchild); createBiTree(T->rchild); } } //前序遍历二叉树并打印 void preTraverse(BiTree T) { if(T) { cout<<T->data<<" "; preTraverse(T->lchild); preTraverse(T->rchild); } } //中序遍历二叉树并打印 void midTraverse(BiTree T) { if(T) { midTraverse(T->lchild); cout<<T->data<<" "; midTraverse(T->rchild); } } //后续遍历二叉树并打印 void postTraverse(BiTree T) { if(T) { postTraverse(T->lchild); postTraverse(T->rchild); cout<<T->data<<" "; } } int main() { BiTree T; //声明一个指向二叉树根节点的指针 createBiTree(T); cout<<"二叉树创建完成!"<<endl; cout<<"前序遍历二叉树:"<<endl; preTraverse(T); cout<<endl; cout<<"中序遍历二叉树:"<<endl; midTraverse(T); cout<<endl; cout<<"后序遍历二叉树:"<<endl; postTraverse(T); return 0; }
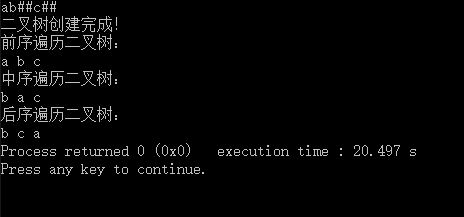
测试结果:
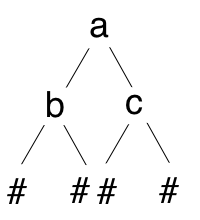
假设我们要建立一个如下图所示的二叉树,#代表空节点,按照前序遍历顺序二叉树表示为:ab##c##
. 
下面是代码的运行结果,正如预期: