zoukankan      html  css  js  c++  java

  • 树链剖分

    树链剖分看起来是个很高级的算法，但实际上很简单。在介绍这个算法之前，要感谢某位大神cgh，是他教了我树链剖分。

    简介

    什么样的题目要用到树链剖分？

    一般是在某些题目中，在一棵树上，求两点的路径上点权（或边权）的最大值（或最小值、和）……
    支持修改权值的操作。（如果不需要改权值可以直接倍增+树上RMQ，见例题三）

    基本思想

    将儿子分为轻儿子、重儿子，将同一条重链上的点集中在一起。用各种数据结构维护（线段树、树状数组、splay）
    以下的讲解使用线段树。

    详细讲解

    一些概念

    1、重儿子和轻儿子

    设x.size表示以x为根的子树的节点个数
    对于每个非叶子节点，size值最大的儿子，就是重儿子。（如果有相同的size，就随便选一个）
    其它的儿子，都是轻儿子。

    2、重链

    重儿子及其父亲连起来，就是重链。
    重链
    如图，灰色的点是重儿子，其它是轻儿子。那几条粗的线就是重链。

    一些性质

    1、若x是轻儿子，x.size<=x.father.size2
    2、从根到某一点的路径上，不超过lg(n)条重链，不超过lg(n)条轻边。

    重点部分

    我们可以将重链上的点在线段树中放在一起。
    例如上面的这棵树，点在线段树中的顺序是：
    1，3，6，10，8，9，7，2，5，4
    加粗的是在重链上的点。重链上的点，在线段树的顺序中要连在一起。
    按照这个顺序，用线段树维护。

    实现细节

    预处理

    首先，使用O(n)的dfs（dfs1），求出depth（深度），father，size，heavy_son（重儿子）。

    然后，再使用O(n)的dfs（dfs2），求出top、to_tree、to_num
    对于点x，若x为重儿子，top为x所在重链的顶端；若x为轻儿子，top=x（可以将每个轻儿子当成一条重链）。
    求top其实很简单，递归时设一个参数k，表示x.top。
    递归给重儿子时，k不变；
    递归给轻儿子时，k为它本身。
    具体见代码。
    对于点x，to_tree表示x在线段树中的位置。对于线段树中的第i个位置，to_num为它对应树中的位置。

    在线操作

    1、修改：直接通过to_tree在线段树中直接修改。
    2、求LCA：见例题一
    3、询问x到y的最大值（或最小值、和……）：见例题二、三

    时间复杂度：O(n+Qlg2n)

    例题一

    描述

    P3379 【模板】最近公共祖先（LCA）

    题目描述

    如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。
    输入输出格式

    输入格式：

    第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。
    接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。
    接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

    输出格式：

    输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

    输入输出样例

    输入样例#1：

    5 5 4
    3 1
    2 4
    5 1
    1 4
    2 4
    3 2
    3 5
    1 2
    4 5

    输出样例#1：

    4
    4
    1
    4
    4

    说明

    时空限制：1000ms,128M
    数据规模：
    对于30%的数据：N<=10，M<=10
    对于70%的数据：N<=10000，M<=10000
    对于100%的数据：N<=500000，M<=500000
    样例说明：
    该树结构如下：
    插图
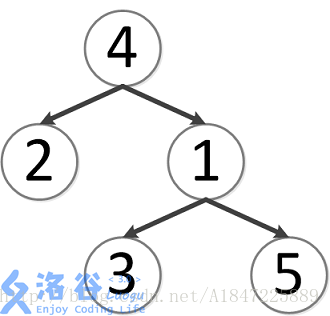
    第一次询问：2、4的最近公共祖先，故为4。
    第二次询问：3、2的最近公共祖先，故为4。
    第三次询问：3、5的最近公共祖先，故为1。
    第四次询问：1、2的最近公共祖先，故为4。
    第五次询问：4、5的最近公共祖先，故为4。
    故输出依次为4、4、1、4、4。

    这是一道LCA的模板题，我曾写过倍增（在线）求LCA和ST（RMQ）算法（在线）求LCA
    现在我们考虑用树链剖分求LCA(x,y)。
    当x.top≠y.top时
    1、选取一个top较深的点k。
    2、k跳到k.top.father。
    这样循环下去，depth较小的点即LCA。

    思考：为什么这么做？
    1、当x.top=y.top时，x和y一定在同一条重链上，那么深度较小的就是LCA。
    2、为什么要选top较深的点而不是它自己较深的点？因为如果选自己较深的那个点，有可能会超过LCA。
    3、为什么跳到k.top.father而不是k.top？因为跳到k.top并不会另一个在同一重链上，跳到k.top.father说明k进入了另一条重链。
    如果还是不懂，可以仔细思考一下。

    因为这题没有点权、边权，可以不用打线段树。

    代码

    #include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,s;
struct EDGE
{
    int to;
    EDGE* las;
} e[1000000];//前向星存边
EDGE* last[500001];

struct Information
{
    int depth,father,size,heavy_son,top;
} d[500001];
void dfs1(int,int,int);//求depth,father,size,heavy_son
void dfs2(int,int);//求top

int LCA(int,int);
int main()
{
    scanf("%d%d%d",&n,&m,&s);
    int i,j=-1,x,y;
    for (i=1;i<n;++i)
    {
        scanf("%d%d",&x,&y);
        e[++j]={y,last[x]};
        last[x]=e+j;
        e[++j]={x,last[y]};
        last[y]=e+j;
    }

    dfs1(0,s,0);
    dfs2(s,s);

    while (m--)
    {
        scanf("%d%d",&x,&y);
        printf("%d
",LCA(x,y));
    }
}

void dfs1(int fa,int x,int de)
{
    d[x]={de,fa,1,0};
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=fa)
        {
            dfs1(x,ei->to,de+1);
            d[x].size+=d[ei->to].size;
            if (d[d[x].heavy_son].size<d[ei->to].size)
                d[x].heavy_son=ei->to;
        }
}
void dfs2(int x,int k)
{
    d[x].top=k;
    if (d[x].heavy_son)
        dfs2(d[x].heavy_son,k);//将k带给重儿子。因为同一重链上的top值相同
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=d[x].father && ei->to!=d[x].heavy_son)
            dfs2(ei->to,ei->to);//轻儿子的top值为它本身
}

int LCA(int x,int y)
{
    for (;d[x].top!=d[y].top;)
    {
        if (d[d[x].top].depth>d[d[y].top].depth)
            x=d[d[x].top].father;
        else 
            y=d[d[y].top].father;
    }
    return d[x].depth<d[y].depth?x:y;
}

    （未完成）

    例题二

    描述

    P2590 [ZJOI2008]树的统计

    题目描述

    一棵树上有n个节点，编号分别为1到n，每个节点都有一个权值w。
    我们将以下面的形式来要求你对这棵树完成一些操作：
    I. CHANGE u t : 把结点u的权值改为t
    II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值
    III. QSUM u v: 询问从点u到点v的路径上的节点的权值和
    注意：从点u到点v的路径上的节点包括u和v本身

    输入格式：

    输入文件的第一行为一个整数n，表示节点的个数。
    接下来n – 1行，每行2个整数a和b，表示节点a和节点b之间有一条边相连。
    接下来一行n个整数，第i个整数wi表示节点i的权值。
    接下来1行，为一个整数q，表示操作的总数。
    接下来q行，每行一个操作，以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。

    输出格式：

    对于每个“QMAX”或者“QSUM”的操作，每行输出一个整数表示要求输出的结果。

    输入输出样例

    输入样例#1：

    4
    1 2
    2 3
    4 1
    4 2 1 3
    12
    QMAX 3 4
    QMAX 3 3
    QMAX 3 2
    QMAX 2 3
    QSUM 3 4
    QSUM 2 1
    CHANGE 1 5
    QMAX 3 4
    CHANGE 3 6
    QMAX 3 4
    QMAX 2 4
    QSUM 3 4

    输出样例#1：

    4
    1
    2
    2
    10
    6
    5
    6
    5
    16

    说明

    对于100％的数据，保证1<=n<=30000，0<=q<=200000；中途操作中保证每个节点的权值w在-30000到30000之间。

    分析

    这是树链剖分的经典例题。这题要求两点之间的和或最大值。
    怎么做？
    观察一下例题一种求LCA的过程，可以发现两个要求的答案其实很相似。
    求LCA时，我们要一条重链一条重链地跳上去。可以类似地，在每次跳上去的时候用线段树求出这一段的和或最大值。
    如果还不懂，那可以套上刚才那流程：
    当x.top≠y.top时
    1、选取一个top较深的点k。
    2、线段树求出k.top到k这条链上的和或最大值，更新答案。k跳到k.top.father。
    这样循环下去。
    设最后depth较小的是a，另一个是b，线段树求出a到b的和或最大值，更新答案。
    这便是最后的答案。

    仔细想想，其实也显然。每次次从k跳到k.top.father时，用k.top到k之间的和或最大值更新答案。
    这样子就可以做到不重复（因为在计算过程中，x和y一定是没有被算过的）。
    最后x和y在同一条链上，它们之间（包括自己）都没有被算过，所以可以直接用线段树来求。

    代码

    #include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
struct EDGE
{
    int to;
    EDGE* las;
} e[60000];//前向星存边
EDGE* last[30001];

struct Information
{
    int depth,father,size,heavy_son,top,to_tree,value;//to_tree表示它在线段树中的编号
} d[30001];
void dfs1(int,int,int);
int to_num[30001],total;//to_num为从线段树中返回原来的编号
void dfs2(int,int);

int a[30001];
struct Node
{
    int MAX,SUM;
} tree[120001];
void build(int,int,int);//建树
void change(int,int,int,int,int);//修改
inline int query_max(int,int);//询问最大值
int Tree_query_max(int,int,int,int,int);//线段树中询问最大值
inline int query_sum(int,int);//询问和
int Tree_query_sum(int,int,int,int,int);//线段树中询问和

int main()
{
    scanf("%d",&n);
    int i,j=-1,x,y;
    for (i=1;i<n;++i)
    {
        scanf("%d %d",&x,&y);
        e[++j]={y,last[x]};
        last[x]=e+j;
        e[++j]={x,last[y]};
        last[y]=e+j;
    }

    dfs1(0,1,0);
    dfs2(1,1);

    for (i=1;i<=n;++i)
        scanf("%d",&d[i].value);
    build(1,1,n);

    int Q;
    scanf("%d",&Q);
    char mode[7];
    while (Q--)
    {
        scanf("%s %d %d",mode,&x,&y);
        switch (mode[1])
        {
            case 'H':
                change(1,1,n,d[x].to_tree,y);
            break;
            case 'M':
                printf("%d
",query_max(x,y));
            break;
            default:
                printf("%d
",query_sum(x,y));
        }
    }
} 

void dfs1(int fa,int x,int de) 
{
    d[x]={de,fa,1};
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=fa)
        {
            dfs1(x,ei->to,de+1);
            d[x].size+=d[ei->to].size;
            if (d[d[x].heavy_son].size<d[ei->to].size)
                d[x].heavy_son=ei->to;
        }
}
void dfs2(int x,int k)
{
    d[x].top=k;
    d[x].to_tree=++total;//对其进行编号。这里有个显然的性质：爸爸的在线段树中编号一定在儿子的前面
    to_num[total]=x;
    if (d[x].heavy_son)
        dfs2(d[x].heavy_son,k);
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=d[x].father && ei->to!=d[x].heavy_son)
            dfs2(ei->to,ei->to);
}

void build(int k,int l,int r)
{
    if (l==r)
    {
        tree[k]={d[to_num[l]].value,d[to_num[l]].value};
        return;
    }
    int mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    tree[k]={max(tree[k<<1].MAX,tree[k<<1|1].MAX),tree[k<<1].SUM+tree[k<<1|1].SUM};
}
void change(int k,int l,int r,int x,int y)
{
    if (l==r)
    {
        tree[k]={y,y};
        return;
    }
    int mid=(l+r)>>1;
    if (x<=mid)
        change(k<<1,l,mid,x,y);
    else
        change(k<<1|1,mid+1,r,x,y);
    tree[k]={max(tree[k<<1].MAX,tree[k<<1|1].MAX),tree[k<<1].SUM+tree[k<<1|1].SUM};
}

inline int query_max(int x,int y)
{
    int ret=-2147483648;
    for (;d[x].top!=d[y].top;)
    {
        if (d[d[x].top].depth>d[d[y].top].depth)
        {
            ret=max(ret,Tree_query_max(1,1,n,d[d[x].top].to_tree,d[x].to_tree));//计算x.top到x之间的最大值 在线段树中，x.top的编号一定在x钱
            x=d[d[x].top].father;
        }
        else 
        {
            ret=max(ret,Tree_query_max(1,1,n,d[d[y].top].to_tree,d[y].to_tree));
            y=d[d[y].top].father;
        }
    }
    if (d[x].depth<d[y].depth)
        ret=max(ret,Tree_query_max(1,1,n,d[x].to_tree,d[y].to_tree));//计算x到y的最大值
    else
        ret=max(ret,Tree_query_max(1,1,n,d[y].to_tree,d[x].to_tree));
    return ret;
}
int Tree_query_max(int k,int l,int r,int st,int en)
{
    if (l==st && r==en)
        return tree[k].MAX;
    int mid=(l+r)>>1;
    if (en<=mid)
        return Tree_query_max(k<<1,l,mid,st,en);
    else if (mid<st)
        return Tree_query_max(k<<1|1,mid+1,r,st,en);
    else
        return max(Tree_query_max(k<<1,l,mid,st,mid),Tree_query_max(k<<1|1,mid+1,r,mid+1,en));
}
inline int query_sum(int x,int y)
{
    int ret=0;
    for (;d[x].top!=d[y].top;)
    {
        if (d[d[x].top].depth>d[d[y].top].depth)
        {
            ret+=Tree_query_sum(1,1,n,d[d[x].top].to_tree,d[x].to_tree);
            x=d[d[x].top].father;
        }
        else 
        {
            ret+=Tree_query_sum(1,1,n,d[d[y].top].to_tree,d[y].to_tree);
            y=d[d[y].top].father;
        }
    }
    if (d[x].depth<d[y].depth)
        ret+=Tree_query_sum(1,1,n,d[x].to_tree,d[y].to_tree);
    else
        ret+=Tree_query_sum(1,1,n,d[y].to_tree,d[x].to_tree);
    return ret;
}
int Tree_query_sum(int k,int l,int r,int st,int en)
{
    if (l==st && r==en)
        return tree[k].SUM;
    int mid=(l+r)>>1;
    if (en<=mid)
        return Tree_query_sum(k<<1,l,mid,st,en);
    else if (mid<st)
        return Tree_query_sum(k<<1|1,mid+1,r,st,en);
    else
        return Tree_query_sum(k<<1,l,mid,st,mid)+Tree_query_sum(k<<1|1,mid+1,r,mid+1,en);
}

    例题三

    描述

    Heatwave

    Description

    　　给你N个点的无向连通图，图中有M条边，第j条边的长度为： d_j.
    　　现在有 K个询问。
    　　每个询问的格式是：A B，表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

    Input

    　　文件名为heatwave.in
    　　第一行： N, M, K。
    　　第2..M+1行: 三个正整数：X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
    　　第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

    Output

    　　对每个询问，输出最长的边最小值是多少。

    Sample Input

    6 6 8
    1 2 5
    2 3 4
    3 4 3
    1 4 8
    2 5 7
    4 6 2
    1 2
    1 3
    1 4
    2 3
    2 4
    5 1
    6 2
    6 1

    Sample Output

    5
    5
    5
    4
    4
    7
    4
    5

    Data Constraint

    50% 1<=N,M<=3000 其中30% K<=5000
    ​100% 1 <= N <= 15,000 　　1 <= M <= 30,000 　　1 <= d_j <= 1,000,000,000 　　1 <= K <= 20,000

    这题并不是个裸题。先说一下解法。
    这题要求所有路径中的最长边的最小值。想让答案最小，显然可以用最小生成树。
    为什么最小生成树是对的？
    其实很显然。假设有两部分点，每一部分的点可以互相到达连起来，
    那么要连接两个区域，就必须走过连同两个区域中的点的一条边。
    这条边当然要越小越好。
    一开始的时候，每一个点都是独立的，最小生成树当然是最好的选择。

    由于这题不需要修改，所以正解是最小生成树+树上RMQ（倍增）。
    树上RMQ类似于且需要倍增（不会倍增的点这里），具体见代码。
    放上树上RMQ（倍增）代码

    #include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int n,m;

struct EDGE_For_MST
{
    int x,y,len;
} em[30001];
bool cmp(const EDGE_For_MST& a,const EDGE_For_MST& b){return a.len<b.len;}
int father[15001];
int getfather(int x)
{
    if (father[x]==x)
        return x;
    return father[x]=getfather(father[x]);
}

struct EDGE
{
    int to,len;
    EDGE* las;
} e[30001];
EDGE* last[15001];

struct Information
{
    int depth;
    int fa[14],MAX[14];
} f[15001];
void dfs(int,int,int,int);

inline int query(int x,int y);
int main()
{
    int Q;
    scanf("%d%d%d",&n,&m,&Q);
    int i;
    for (i=1;i<=m;++i)
        scanf("%d%d%d",&em[i].x,&em[i].y,&em[i].len);
    //最小生成树
    sort(em+1,em+m+1,cmp);
    for (i=1;i<=n;++i)
        father[i]=i;
    int j=0,k=0,xx,yy;
    for (i=1;i<=m;++i)
    {
        xx=getfather(em[i].x);
        yy=getfather(em[i].y);
        if (xx!=yy)
        {
            father[xx]=yy;
            e[++k]={em[i].y,em[i].len,last[em[i].x]};
            last[em[i].x]=e+k;
            e[++k]={em[i].x,em[i].len,last[em[i].y]};
            last[em[i].y]=e+k;
            if (++j==n-1)
                break;
        }
    }
    //树上RMQ求答案
    dfs(0,0,1,0);
    int ans;
    for (;Q;--Q)
    {
        scanf("%d%d",&xx,&yy);
        printf("%d
",query(xx,yy));
    }
} 
void dfs(int len,int father,int x,int de)
{
    f[x].depth=de;
    f[x].fa[0]=father;
    f[x].MAX[0]=len;
    int i,j;
    for (i=1,j=2;j<=de;++i,j<<=1)
    {
        f[x].fa[i]=f[f[x].fa[i-1]].fa[i-1];
        f[x].MAX[i]=max(f[x].MAX[i-1],f[f[x].fa[i-1]].MAX[i-1]);
    }
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (father!=ei->to)
            dfs(ei->len,x,ei->to,de+1);
}
inline int query(int x,int y)
{
    if (f[x].depth<f[y].depth)
        swap(x,y);
    int ret=0,i=0,k=f[x].depth-f[y].depth;
    while (k)
    {
        if (k&1)
        {
            ret=max(ret,f[x].MAX[i]);
            x=f[x].fa[i];
        }
        k>>=1;
        ++i;
    }
    if (x==y)
        return ret;
    for (i=int(log2(f[x].depth));i>=0;--i)
        if (f[x].fa[i]!=f[y].fa[i])
        {
            ret=max({ret,f[x].MAX[i],f[y].MAX[i]});
            x=f[x].fa[i];
            y=f[y].fa[i];
        }
    return max({ret,f[x].MAX[0],f[y].MAX[0]});
}

    其实这题可以用树链剖分很好地解决。
    最小生成树后，就和例题二差不多了。只是例题二求点权的和或最大值，这题求边权的和或最大值。
    其实把点转换成边很简单。将每条边的权值放在与此边连的儿子上，就能成功将边权转换成点权。
    求的时候跟例题二一样，只是不需要算LCA(x,y)的点权罢了。

    #include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int n,m;

struct EDGE_For_MST
{
    int x,y,len;
} em[30001];
bool cmp(const EDGE_For_MST& a,const EDGE_For_MST& b){return a.len<b.len;}
int father[15001];
int getfather(int x)
{
    if (father[x]==x)
        return x;
    return father[x]=getfather(father[x]);
}

struct EDGE
{
    int to,len;
    EDGE* las;
} e[30001];
EDGE* last[15001];

struct Information
{
    int depth,father,size,heavy_son,top,to_tree,value;
} d[15001];
void dfs1(int,int,int,int);
int to_num[15001],total;
void dfs2(int,int);

int tree[60001];
void build(int,int,int);

inline int query(int,int);
int Tree_query(int,int,int,int,int);
int main()
{
    int Q;
    scanf("%d%d%d",&n,&m,&Q);
    int i;
    for (i=1;i<=m;++i)
        scanf("%d%d%d",&em[i].x,&em[i].y,&em[i].len);
    //最小生成树
    sort(em+1,em+m+1,cmp);
    for (i=1;i<=n;++i)
        father[i]=i;
    int j=0,k=0,xx,yy;
    for (i=1;i<=m;++i)
    {
        xx=getfather(em[i].x);
        yy=getfather(em[i].y);
        if (xx!=yy)
        {
            father[xx]=yy;
            e[++k]={em[i].y,em[i].len,last[em[i].x]};
            last[em[i].x]=e+k;
            e[++k]={em[i].x,em[i].len,last[em[i].y]};
            last[em[i].y]=e+k;
            if (++j==n-1)
                break;
        }
    }
    //树链剖分
    dfs1(0,0,1,0);
    dfs2(1,1);
    build(1,1,n);

    while (Q--)
    {
        scanf("%d%d",&xx,&yy);
        printf("%d
",query(xx,yy));    
    } 
} 

void dfs1(int le,int fa,int x,int de)
{
    d[x]={de,fa,1,0,0,0,le};
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=fa)
        {
            dfs1(ei->len,x,ei->to,de+1);
            d[x].size+=d[ei->to].size;
            if (d[d[x].heavy_son].size<d[ei->to].size)
                d[x].heavy_son=ei->to;
        }
}
void dfs2(int x,int k)
{
    d[x].top=k;
    d[x].to_tree=++total;
    to_num[total]=x;
    if (d[x].heavy_son)
        dfs2(d[x].heavy_son,k);
    EDGE* ei;
    for (ei=last[x];ei;ei=ei->las)
        if (ei->to!=d[x].father && ei->to!=d[x].heavy_son)
            dfs2(ei->to,ei->to);
}
void build(int k,int l,int r)
{
    if (l==r)
    {
        tree[k]=d[to_num[l]].value;
        return;
    }
    int mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    tree[k]=max(tree[k<<1],tree[k<<1|1]);
}

inline int query(int x,int y)
{
    int ret=0;
    for (;d[x].top!=d[y].top;)
        if (d[d[x].top].depth>d[d[y].top].depth)
        {
            ret=max(ret,Tree_query(1,1,n,d[d[x].top].to_tree,d[x].to_tree));
            x=d[d[x].top].father;
        }
        else
        {
            ret=max(ret,Tree_query(1,1,n,d[d[y].top].to_tree,d[y].to_tree));
            y=d[d[y].top].father;
        }
    if (x==y)//若x==y，那么线段树询问时l>r，会RE
        return ret;
    if (d[x].depth<d[y].depth)
        ret=max(ret,Tree_query(1,1,n,d[d[x].heavy_son].to_tree,d[y].to_tree));
    else
        ret=max(ret,Tree_query(1,1,n,d[d[y].heavy_son].to_tree,d[x].to_tree));
    return ret;
}
int Tree_query(int k,int l,int r,int st,int en)
{
    if (l==st && r==en)
        return tree[k];
    int mid=(l+r)>>1;
    if (en<=mid)
        return Tree_query(k<<1,l,mid,st,en);
    else if (mid<st)    
        return Tree_query(k<<1|1,mid+1,r,st,en);
    else
        return max(Tree_query(k<<1,l,mid,st,mid),Tree_query(k<<1|1,mid+1,r,mid+1,en));
}

    总结

    1、 当遇到求树上两点间的路径上，点权或边权的和（最大值、最小值……）的题目时，可以用树链剖分。
    2、 树链剖分支持修改点权、边权的操作，但不支持删边、删点操作（要这么做就得用LCT）
    3、 树链剖分就是将点分成几部分，同是重链的点在线段树（或其它数据结构）中的编号连在一起，用线段树（或其它数据结构维护）。
  • 相关阅读:
    linux下文件的复制、移动与删除
    Hbase万亿级存储性能优化总结-配置
    hbase 读写和优化
    hive数据倾斜定位及处理
    flink初识及安装flink standalone集群
    【Linux】用less查看日志文件
    sqoop的详细使用及原理
    HBase删除数据的原理
    hbase数据加盐（Salting）存储与协处理器查询数据的方法
    Hbase内存磁盘大致关系
  • 原文地址：https://www.cnblogs.com/jz-597/p/11145306.html
Copyright © 2011-2022 走看看